hàm số lượng giác 11

1. Định nghĩa hàm con số giác

• Quy tắc bịa đặt ứng từng số thực x với số thực sinx được gọi là hàm số sin, kí hiệu nó = sinx. Tập xác lập của hàm số sin là \(\mathbb{R}\).
• Quy tắc bịa đặt ứng từng số thực x với số thực cosx được gọi là hàm số cos, kí hiệu nó = cosx. Tập xác lập của hàm số côsin là \(\mathbb{R}\).
• Hàm số cho tới vì như thế công thức \(y = \frac{{\sin \alpha }}{{\cos \alpha }}\)được gọi là hàm số tang, kí hiệu là nó = tanx. Tập xác lập của hàm số tang là \(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi |k \in \mathbb{Z}} \right\}\).
• Hàm số cho tới vì như thế công thức \(y = \frac{{\cos \alpha }}{{\sin \alpha }}\)được gọi là hàm số côtang, kí hiệu là nó = cotx. Tập xác lập của hàm số côtang là \(\mathbb{R}\backslash \left\{ {k\pi |k \in \mathbb{Z}} \right\}\).

2. Hàm số chẵn, hàm số lẻ, hàm số tuần hoàn

a, Hàm số chẵn, hàm số lẻ

Cho hàm số nó = f(x) đem tập dượt xác lập là D.

• Hàm số f(x) được gọi là hàm số chẵn nếu như \(\forall x \in D\) thì \( - x \in D\) và \(f( - x) = f(x)\). Đồ thị của một hàm số chẵn nhận trục tung (Oy) thực hiện trục đối xứng.
• Hàm số f(x) được gọi là hàm số lẻ nếu như \(\forall x \in D\) thì \( - x \in D\) và \(f( - x) =  - f(x)\). Đồ thị của một hàm số lẻ nhận gốc tọa phỏng thực hiện tâm đối xứng.

b, Hàm số tuần hoàn

Hàm số nó = f(x) đem tập dượt xác lập D được gọi là hàm số tuần trả nếu như tồn bên trên số T \( \ne \)0 sao cho tới với từng \(x \in D\)ta có:

• \(x + T \in D\)và \(x - T \in D\)
• \(f(x + T) = f(x)\)

Số T dương nhỏ nhất vừa lòng cơ hội ĐK bên trên (nêu có) được gọi là chu kì của hàm số tuần trả bại.

* Nhận xét:

Các hàm số nó = sinx, y=cosx tuần trả chu kì 2\(\pi \).

Xem thêm: cách sử dụng google drive

Các hàm số nó = tanx, y=cotx tuần trả chu kì \(\pi \).

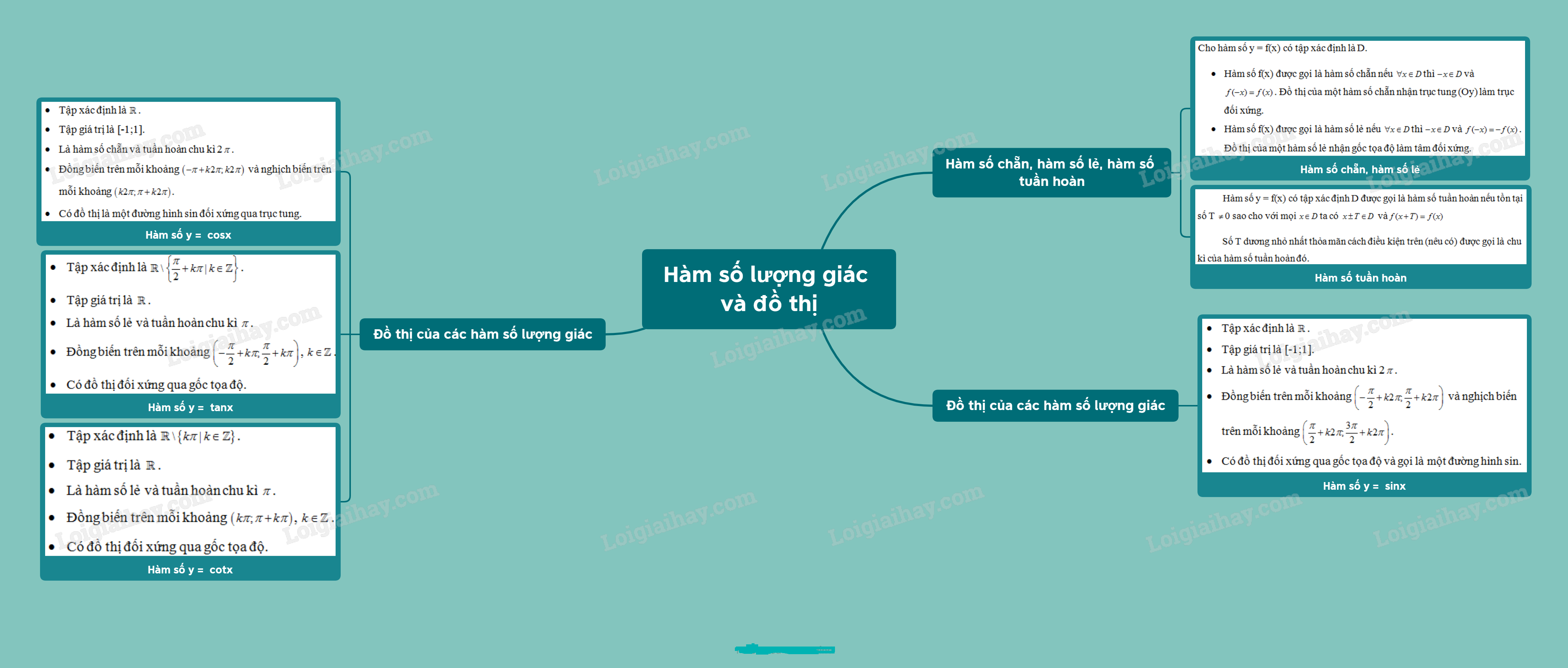
3. Đồ thị và đặc điểm của hàm số nó =  sinx

• Tập xác lập là \(\mathbb{R}\).
• Tập độ quý hiếm là [-1;1].
• Là hàm số lẻ và tuần trả chu kì 2\(\pi \).
• Đồng đổi mới bên trên từng khoảng tầm \(\left( { - \frac{\pi }{2} + k2\pi ;\frac{\pi }{2} + k2\pi } \right)\) và nghịch ngợm đổi mới bên trên từng khoảng tầm \(\left( {\frac{\pi }{2} + k2\pi ;\frac{{3\pi }}{2} + k2\pi } \right)\).
• Có đồ vật thị đối xứng qua chuyện gốc tọa phỏng và gọi là 1 lối hình sin.

4. Đồ thị và đặc điểm của hàm số nó =  cosx

• Tập xác lập là \(\mathbb{R}\).
• Tập độ quý hiếm là [-1;1].
• Là hàm số chẵn và tuần trả chu kì 2\(\pi \).
• Đồng đổi mới bên trên từng khoảng tầm \(\left( { - \pi  + k2\pi ;k2\pi } \right)\) và nghịch ngợm đổi mới bên trên từng khoảng tầm \(\left( {k2\pi ;\pi  + k2\pi } \right)\).
• Có đồ vật thị là 1 lối hình sin đối xứng qua chuyện trục tung.

5. Đồ thị và đặc điểm của hàm số nó =  tanx

• Tập xác lập là \(\mathbb{R}\backslash \left\{ {\frac{\pi }{2} + k\pi |k \in \mathbb{Z}} \right\}\).
• Tập độ quý hiếm là \(\mathbb{R}\).
• Là hàm số lẻ và tuần trả chu kì \(\pi \).
• Đồng đổi mới bên trên từng khoảng tầm \(\left( { - \frac{\pi }{2} + k\pi ;\frac{\pi }{2} + k\pi } \right)\), \(k \in \mathbb{Z}\).
• Có đồ vật thị đối xứng qua chuyện gốc tọa phỏng.

6. Đồ thị và đặc điểm của hàm số nó =  cotx

• Tập xác lập là \(\mathbb{R}\backslash \left\{ {k\pi |k \in \mathbb{Z}} \right\}\).
• Tập độ quý hiếm là \(\mathbb{R}\).
• Là hàm số lẻ và tuần trả chu kì \(\pi \).
• Đồng đổi mới bên trên từng khoảng tầm \(\left( {k\pi ;\pi  + k\pi } \right)\), \(k \in \mathbb{Z}\).
• Có đồ vật thị đối xứng qua chuyện gốc tọa phỏng.
• 

Bình luận

Chia sẻ