Chủ đề công thức tính cạnh tam giác vuông: Công thức tính cạnh tam giác vuông kể từ toan lý Pytago là một trong trong mỗi công thức cần thiết vô toán học tập. Nó được cho phép tất cả chúng ta tính được phỏng lâu năm cạnh huyền của một tam giác vuông chỉ trải qua những vấn đề về nhì cạnh góc vuông. Đây là một trong công thức hữu ích và tiện lợi, giúp chúng ta giải quyết và xử lý những câu hỏi tương quan cho tới tam giác vuông một cơ hội nhanh gọn và đúng chuẩn.
Có công thức ví dụ nào là nhằm tính cạnh của tam giác vuông không?
Có một công thức ví dụ nhằm tính phỏng lâu năm cạnh của một tam giác vuông dùng toan lý Pythagoras. Định lý Pythagoras cho thấy rằng vô một tam giác vuông, bình phương phỏng lâu năm cạnh huyền bởi vì tổng bình phương phỏng lâu năm nhì cạnh góc vuông.
Công thức nhằm tính cạnh huyền (c) của tam giác vuông được mang đến bởi:
c = √(a^2 + b^2)
Trong cơ, a và b là phỏng lâu năm nhì cạnh góc vuông của tam giác vuông.
Để đo lường, tớ chỉ việc bình phương phỏng lâu năm nhì cạnh góc vuông, tiếp sau đó nằm trong bọn chúng lại và lấy căn bậc nhì của tổng nhằm tìm hiểu phỏng lâu năm cạnh huyền.
Ví dụ, nếu như tớ đem tam giác vuông có tính lâu năm nhì cạnh góc vuông là a = 3 và b = 4, tớ rất có thể tính phỏng lâu năm cạnh huyền (c) như sau:
c = √(3^2 + 4^2)
= √(9 + 16)
= √25
= 5
Vậy phỏng lâu năm cạnh huyền của tam giác vuông này là 5.
Bạn đang xem: công thức định lý pytago
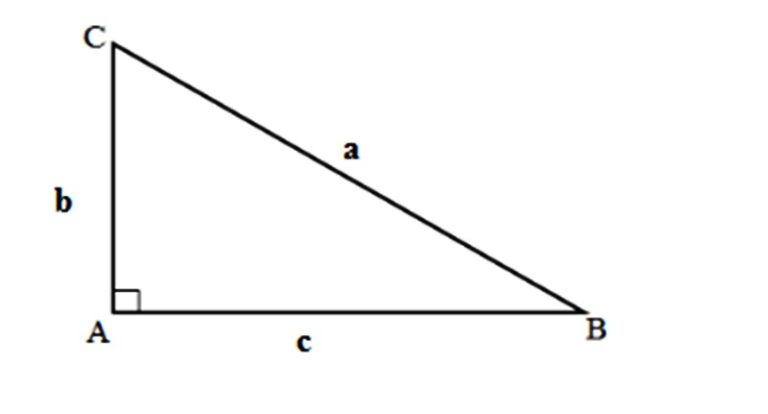
Định lý Pytago là gì và được vận dụng ra sao trong công việc tính cạnh tam giác vuông?
Định lý Pytago, hoặc thường hay gọi là toan lý Pythagoras, là một trong toan lý cần thiết vô toán học tập tế bào miêu tả quan hệ trong những cạnh của một tam giác vuông. Định lý này bảo rằng vô một tam giác vuông, bình phương của cạnh huyền (cạnh đối lập với góc vuông) bởi vì tổng bình phương của nhì cạnh góc vuông.
Cụ thể, công thức của toan lý Pytago được trình diễn như sau:
c^2 = a^2 + b^2
Trong đó:
- c là phỏng lâu năm của cạnh huyền (cạnh đối lập với góc vuông).
- a và b là phỏng lâu năm của nhì cạnh góc vuông.
Với công thức này, tất cả chúng ta rất có thể đo lường phỏng lâu năm của một cạnh chưa chắc chắn vô tam giác vuông lúc biết phỏng lâu năm của nhì cạnh không giống.
Ví dụ minh họa:
Giả sử tất cả chúng ta mang trong mình 1 tam giác vuông với phỏng lâu năm của những cạnh góc vuông là a = 3 và b = 4. Để tính phỏng lâu năm của cạnh huyền (c), tất cả chúng ta dùng công thức của toan lý Pytago:
c^2 = a^2 + b^2
c^2 = 3^2 + 4^2
c^2 = 9 + 16
c^2 = 25
Đặt một c là căn bậc nhì của 25, tớ có:
c = căn bậc nhì của 25
c = 5
Vậy, phỏng lâu năm của cạnh huyền vô tam giác vuông này là 5.
Định lý Pytago được vận dụng rộng thoải mái trong công việc giải quyết và xử lý những yếu tố tương quan cho tới những tam giác vuông. Với công thức này, tất cả chúng ta rất có thể đo lường phỏng lâu năm những cạnh vô tam giác, tìm hiểu rời khỏi những tỉ trọng trong những cạnh, và vận dụng trong vô số nhiều nghành như xây đắp, kiến thiết, và vật lý cơ.
Ngoài toan lý Pytago, còn tồn tại những công thức nào là không giống nhằm tính cạnh tam giác vuông?
Ngoài toan lý Pytago, còn tồn tại một số trong những công thức không giống nhằm tính cạnh tam giác vuông. Dưới đó là một số trong những công thức phổ biến:
1. Công thức của toan lý Pytago: Định lý Pytago bảo rằng tổng của bình phương nhì cạnh góc vuông vô tam giác vuông bởi vì bình phương của cạnh huyền (c). Công thức này rất có thể được viết lách bên dưới dạng: c^2 = a^2 + b^2, vô cơ c là cạnh huyền và a, b là nhì cạnh góc vuông.
2. Công thức số học: Trong một tam giác vuông cân nặng, từng cạnh đều phải có phỏng lâu năm cân nhau. Vì vậy, nhằm tính cạnh tam giác vuông cân nặng, tớ rất có thể dùng công thức c = a, vô cơ c là cạnh huyền và a là cạnh góc vuông.
3. Công thức hình học: Trong một tam giác vuông cân nặng, đàng cao (h) trải qua cạnh huyền và phân chia nó trở thành nhì phần cân nhau. Với công thức này, tớ rất có thể tính cạnh tam giác vuông cân nặng bằng phương pháp dùng công thức a = h/√2, vô cơ a là cạnh góc vuông và h là đàng cao.
4. Công thức Pythagoreans: Công thức này được dùng nhằm tính cạnh huyền của tam giác vuông lúc biết phỏng lâu năm nhì cạnh góc vuông. Công thức này còn có dạng c = √(a^2 + b^2), vô cơ c là cạnh huyền và a, b là nhì cạnh góc vuông.
Những công thức này rất có thể được dùng nhằm tính cạnh trong những tam giác vuông và tam giác vuông cân nặng.

Cạnh Huyền Là Gì - 3 Cách Tính Cạnh Huyền Tam Giác Vuông - Toán Học
Cạnh Huyền Tam Giác Vuông: Hãy tò mò kín ở phía đằng sau Cạnh Huyền Tam Giác Vuông vô video clip tuyệt hảo này! Hiểu rõ rệt tại vì sao cạnh huyền là nhân tố cần thiết vô tam giác vuông và phần mềm của chính nó vô cuộc sống đời thường hằng ngày của tất cả chúng ta. Xem ngay lập tức nhằm trở nên Chuyên Viên toán học tập thực thụ!
Lấy ví dụ và chỉ dẫn phương pháp tính cạnh huyền của tam giác vuông bằng phương pháp dùng toan lý Pytago.
Để tính cạnh huyền của một tam giác vuông bằng phương pháp dùng toan lý Pytago, tớ rất có thể tuân theo công việc sau:
Bước 1: Xác toan nhì cạnh góc vuông của tam giác
Đầu tiên, tớ cần thiết xác lập nhì cạnh góc vuông của tam giác. Đây là nhì cạnh đem lượng 90 phỏng cùng nhau.
Ví dụ, fake sử tớ mang trong mình 1 tam giác vuông với cạnh a là 3 và cạnh b là 4. Ta cần thiết tính cạnh huyền của tam giác này.
Bước 2: kề dụng công thức toan lý Pytago
Công thức của toan lý Pytago là a^2 + b^2 = c^2, vô cơ c là cạnh huyền của tam giác vuông.
Áp dụng công thức này vô ví dụ của tất cả chúng ta, tớ đem 3^2 + 4^2 = c^2.
Bước 3: Tính độ quý hiếm của cạnh huyền
Tiếp theo đuổi, tớ tính độ quý hiếm của c^2 bằng phương pháp thay cho thế những độ quý hiếm tiếp tục biết vô công thức.
Ta đem 3^2 + 4^2 = c^2, tức là 9 + 16 = c^2.
Tổng của 9 và 16 là 25, vậy c^2 = 25.
Bước 4: Tìm độ quý hiếm của cạnh huyền
Cuối nằm trong, tớ tính căn bậc nhì của độ quý hiếm của c^2 nhằm tìm hiểu độ quý hiếm của cạnh huyền.
Trong ví dụ của tất cả chúng ta, căn bậc nhì của 25 là 5.
Vậy cạnh huyền của tam giác vuông với cạnh a là 3 và cạnh b là 4 là 5.
Tóm lại, nhằm tính cạnh huyền của tam giác vuông bằng phương pháp dùng toan lý Pytago, tớ tiến hành công việc sau: xác lập nhì cạnh góc vuông, vận dụng công thức Pytago, tính độ quý hiếm của cạnh huyền và tìm hiểu độ quý hiếm sau cuối.
Làm thế nào là nhằm tính cạnh góc vuông của tam giác vuông lúc biết cạnh huyền và một cạnh góc vuông?
Để tính cạnh góc vuông của tam giác vuông lúc biết cạnh huyền và một cạnh góc vuông, tớ rất có thể dùng toan lý Pytago. Định lý Pytago tế bào miêu tả quan hệ trong những cạnh của một tam giác vuông.
Cách tính cạnh góc vuông rất có thể được tiến hành như sau:
1. Xác toan cạnh huyền và cạnh góc vuông của tam giác vuông.
2. kề dụng công thức vô toan lý Pytago, tớ có: c^2 = a^2 + b^2. Trong số đó, c là cạnh huyền, a và b là nhì cạnh góc vuông.
3. Thay những độ quý hiếm tiếp tục biết vô công thức. Ví dụ, nếu như tớ biết cạnh huyền là 5 và một cạnh góc vuông là 3, tớ có: c^2 = 3^2 + b^2.
4. Giải phương trình nhằm tìm hiểu độ quý hiếm của b. Với ví dụ bên trên, tớ có: c^2 = 9 + b^2 → 5^2 = 9 + b^2 → 25 = 9 + b^2 → b^2 = 16 → b = 4.
5. Do cơ, cạnh góc vuông của tam giác vuông là 4.
Xem thêm: game nhiều người chơi nhất
_HOOK_
Định Lý Pythagore Trong Tam Giác Vuông - Tính Độ Dài Cạnh - Toán Lớp 7 - P1
Định Lý Pythagore: Bạn mong muốn tìm hiểu hiểu về một trong mỗi toan lý cần thiết nhất vô toán học? Video này tiếp tục phân tích và lý giải cụ thể về Định Lý Pythagore và phần mềm thực tiễn của chính nó. Hãy nằm trong tò mò những tuyệt kỹ toán học tập thú vị này và nâng lên kỹ năng của bạn!
Tính cạnh huyền của một tam giác vuông lúc biết phỏng lâu năm nhì cạnh góc vuông.
Công thức tính cạnh huyền của một tam giác vuông lúc biết phỏng lâu năm nhì cạnh góc vuông được dựa vào toan lý Pythagoras. Định lý Pythagoras cho thấy rằng bình phương của cạnh huyền bởi vì tổng bình phương của nhì cạnh góc vuông.
Để tính cạnh huyền (c) của tam giác vuông, tớ thực hiện như sau:
1. Xác toan phỏng lâu năm của những cạnh góc vuông a và b.
2. Sử dụng công thức c = √(a^2 + b^2) nhằm tính cạnh huyền.
Ví dụ: Giả sử tớ mang trong mình 1 tam giác vuông có tính lâu năm cạnh góc vuông a = 3 centimet và cạnh góc vuông b = 4 centimet. Ta tiếp tục tính phỏng lâu năm cạnh huyền c của tam giác.
Áp dụng công thức c = √(a^2 + b^2), tớ có:
c = √(3^2 + 4^2)
= √(9 + 16)
= √25
= 5 centimet.
Vậy, với tam giác vuông có tính lâu năm nhì cạnh góc vuông là a = 3 centimet và b = 4 centimet, cạnh huyền của tam giác là c = 5 centimet.
Giải quí cơ hội dùng công thức Pytago nhằm tính cạnh vuông góc của tam giác vuông Khi chỉ biết cạnh huyền.
Để tính cạnh vuông góc của tam giác vuông Khi chỉ biết cạnh huyền, tất cả chúng ta rất có thể dùng công thức Pythagoras.
Công thức Pythagoras là công thức cần thiết vô toán học tập khái niệm quan hệ đằm thắm 3 cạnh của một tam giác vuông. Công thức này bảo rằng tổng bình phương của nhì cạnh góc nhọn của tam giác vuông bởi vì bình phương của cạnh huyền.
Theo toan lý Pythagoras, tớ đem công thức: cạnh huyền bình phương = cạnh góc nhọn loại nhất bình phương + cạnh góc nhọn loại nhì bình phương.
Với tam giác vuông, cạnh huyền là cạnh lớn số 1, là đàng chéo cánh của tam giác. Vì vậy, nếu như tất cả chúng ta chỉ biết cạnh huyền và mong muốn tính cạnh vuông góc, tớ nên biết nhì cạnh góc nhọn.
Để tính cạnh vuông góc, tớ cần thiết căn bậc nhì của tổng bình phương nhì cạnh góc nhọn. Công thức tiếp tục là:
cạnh vuông góc = căn bậc nhì của (cạnh huyền^2 - cạnh góc nhọn 1^2)
Ví dụ, nếu như tớ biết cạnh huyền của tam giác vuông là 5 và cạnh góc nhọn loại nhất là 3, tớ rất có thể tính cạnh vuông góc bằng phương pháp sau:
cạnh vuông góc = căn bậc nhì của (5^2 - 3^2)
= căn bậc nhì của (25 - 9)
= căn bậc nhì của 16
= 4
Vậy, cạnh vuông góc của tam giác vuông này là 4.
Có công thức nào là không giống nhằm tính cạnh góc vuông của tam giác vuông không?
Có, ngoài công thức tính cạnh huyền tam giác vuông bởi vì toan lý Pytago, còn tồn tại công thức tính cạnh góc vuông của tam giác vuông bởi vì toan lý Pitago. Công thức này được dùng Khi tớ tiếp tục biết phỏng lâu năm cạnh và đàng cao của tam giác vuông. Để tính cạnh góc vuông của tam giác vuông bởi vì công thức này, tớ cần thiết thực hiện công việc sau:
1. Xác toan phỏng lâu năm cạnh và đàng cao của tam giác vuông.
2. kề dụng công thức của toan lý Pitago: c^2 = a^2 + b^2, vô cơ c là cạnh huyền, a và b theo thứ tự là những cạnh còn sót lại của tam giác và được xem bởi vì đàng cao và phỏng lâu năm cạnh tiếp tục biết.
3. Tiến hành đo lường nhằm tìm hiểu rời khỏi phỏng lâu năm cạnh huyền, c.
Ví dụ: Cho tam giác vuông đem đàng cao là 3 và cạnh là 4.
Áp dụng công thức toan lý Pitago: c^2 = a^2 + b^2
c^2 = 3^2 + 4^2
c^2 = 9 + 16
c^2 = 25
Do cơ, c = căn bậc nhì của 25.
c = 5
Vậy, phỏng lâu năm cạnh huyền của tam giác vuông là 5.
Tính Cạnh Huyền Trong Tam Giác Vuông
Tính Cạnh Huyền: Bạn vẫn muốn tìm hiểu hiểu phương pháp tính cạnh huyền của một tam giác vuông nhưng mà ko cần thiết công thức phức tạp? Trong video clip này, công ty chúng tôi tiếp tục hỗ trợ cho chính mình một cách thức đơn giản và giản dị và dễ dàng nắm bắt nhằm tính cạnh huyền. Hãy coi ngay lập tức và trở nên người xuất sắc toán nhanh chóng chóng!
Xem thêm: tên game hay cho nữ
Tính cạnh mặt mũi của tam giác vuông lúc biết cạnh góc vuông và cạnh huyền.
Để tính cạnh mặt mũi của một tam giác vuông Khi tiếp tục biết cạnh huyền và cạnh góc vuông, tất cả chúng ta rất có thể dùng toan lý Pythagore.
Định lý Pythagore cho thấy rằng vô một tam giác vuông, bình phương của phỏng lâu năm cạnh huyền (được ký hiệu là c) bởi vì tổng bình phương của phỏng lâu năm nhì cạnh góc vuông (được ký hiệu là a và b).
Công thức toan lý Pythagore:
c^2 = a^2 + b^2
Đầu tiên, xác lập độ quý hiếm của cạnh góc vuông và cạnh huyền vô tam giác vuông của người sử dụng. Giả sử cạnh góc vuông được ký hiệu là a và cạnh huyền được ký hiệu là c.
Tiếp theo đuổi, thay cho độ quý hiếm vô công thức:
c^2 = a^2 + b^2
Vì chúng ta tiếp tục biết cạnh góc vuông và cạnh huyền, chúng ta có thể tính giá tốt trị của cạnh mặt mũi (b) bằng phương pháp dùng công thức bên trên.
Bước sau cuối là lấy căn bậc nhì của độ quý hiếm bình phương của cạnh mặt mũi (b) nhằm tìm hiểu rời khỏi phỏng lâu năm thực tiễn của cạnh mặt mũi.
Chẳng hạn, nếu như cạnh góc vuông (a) là 3 và cạnh huyền (c) là 5, tớ rất có thể tính độ quý hiếm của cạnh mặt mũi như sau:
c^2 = a^2 + b^2
5^2 = 3^2 + b^2
25 = 9 + b^2
b^2 = 25 - 9
b^2 = 16
b = √16
b = 4
Vậy cạnh mặt mũi của tam giác vuông vô tình huống này còn có phỏng lâu năm là 4.
Thực hành: Tính toán những độ quý hiếm cạnh và góc của một tam giác vuông dựa vào công thức tính cạnh.
Để đo lường những độ quý hiếm cạnh và góc của một tam giác vuông dựa vào công thức tính cạnh, tớ rất có thể dùng toan lý Pytago.
Định lý Pytago bảo rằng vô một tam giác vuông, bình phương của cạnh huyền (cạnh đối lập góc vuông) bởi vì tổng bình phương của nhì cạnh góc vuông (cạnh góc vuông kề và cạnh góc vuông đối diện). Công thức tính cạnh tam giác vuông là:
c² = a² + b²
Trong đó:
- c là cạnh huyền (cạnh đối lập góc vuông)
- a và b là nhì cạnh góc vuông (cạnh góc vuông kề và cạnh góc vuông đối diện)
Ta rất có thể đo lường độ quý hiếm cạnh và góc của một tam giác vuông bằng phương pháp vận dụng công thức tính cạnh pytago và dùng những độ quý hiếm tiếp tục biết.
Ví dụ:
- Cho tam giác vuông ABC với cạnh góc vuông AB = 3 centimet và cạnh góc vuông AC = 4 centimet. Ta cần thiết đo lường cạnh huyền BC và những góc.
Bước 1: Sử dụng công thức tính cạnh pytago nhằm đo lường cạnh huyền BC:
BC² = AB² + AC²
BC² = 3² + 4²
BC² = 9 + 16
BC = căn bậc nhì của (9 + 16)
BC = căn bậc nhì của 25
BC = 5 cm
Bước 2: Tính toán những góc vô tam giác vuông:
- Góc A: Là góc vuông, có mức giá trị là 90 phỏng.
- Góc B: Là góc ngược với cạnh BC (cạnh huyền), tớ rất có thể đo lường góc này bởi vì công thức:
sin(B) = AB/BC
sin(B) = 3/5
B = arcsin(3/5)
B = 36.87 phỏng (khoảng thực hiện tròn)
- Góc C: Là góc ngược với cạnh AC, tớ rất có thể đo lường góc này bởi vì công thức:
sin(C) = AC/BC
sin(C) = 4/5
C = arcsin(4/5)
C = 53.13 phỏng (khoảng thực hiện tròn)
Vậy, vô tam giác vuông ABC với cạnh góc vuông AB = 3 centimet và cạnh góc vuông AC = 4 centimet, tớ đem cạnh huyền BC = 5 centimet và những góc A = 90 phỏng, B = 36.87 phỏng, C = 53.13 phỏng.
_HOOK_











Bình luận