thể tích nón cụt

Trong nội dung bài viết thời điểm hôm nay, bản thân tiếp tục share một chủ thể khá hoặc là hình nón cụt. Quý khách hàng từng nghe hoặc biết cho tới những công thức tính diện tích S hoặc thể tích của hình nón cụt chưa? Nếu ko và chúng ta đang được quan hoài thì nằm trong bản thân coi nội dung nội dung bài viết này nhé bởi vì nó được viết lách rời khỏi giành riêng cho những người dân như chúng ta ê. Bắt đầu nào

Hình chóp cụt là gì?

Là một tình huống quan trọng của hình chóp Khi tớ sử dụng một phía phẳng lặng tưởng tượng tuy vậy song với mặt mũi lòng của hình chóp nhằm hạn chế. Nghĩa là hình chóp cụt nhì mặt mũi lòng tuy vậy song cùng nhau (quan sát hình dưới)

Bạn đang xem: thể tích nón cụt

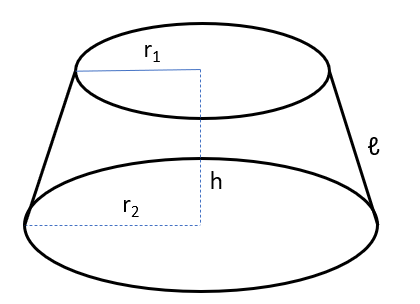
Từ hình vẽ bên trên, tớ thấy

• Các mặt mũi lòng chóp cụt là hình tròn
• Nó với nhì mặt mũi lòng nửa đường kính ko cân nhau r₂ > r₁(nếu vày thìa là hình trụ)
• h là khoảng cách kể từ mặt mũi lòng nửa đường kính r₂ cho tới mặt mũi lòng nửa đường kính r₁
• ℓ được gọi là lối sinh của hình chóp cụt

Thể tích hình nón cụt

Nếu chúng ta hiểu rằng diện tích S hoặc nửa đường kính của 2 mặt mũi lòng hình nón cụt thì thể tích của chính nó được xác lập theo dõi công thức tổng quát:

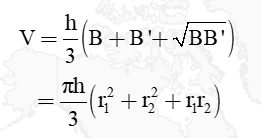
Giải thích:

• B; B’ thứu tự là diện tích S của 2 mặt mũi lòng (thường đơn vị chức năng là m²)
• h là khoảng cách sớm nhất thân ái 2 mặt mũi lòng ( hoặc thường hay gọi là chiều cao), đơn vị chức năng là m
• π = 3,1416
• V là thể tích của khối chóp cụt (m³)
• r₁; r₂ thứu tự là nửa đường kính của những mặt mũi lòng (m)

Diện tích hình nón cụt

Khi phát biểu cho tới diện tích S của khối nón cụt tớ lưu ý ngay lập tức 2 công thức là

• Diện tích xung quanh

• Diện tích toàn phần

Lưu ý: Đường sinh ℓ được xem theo dõi công thức $\ell = \sqrt {{h^2} + {{\left( {{r_2} – {r_1}} \right)}^2}} $

Bài tập

Bài tập dượt 1. Một hình chóp cụt với những thông số kỹ thuật như hình vẽ. Hãy lần thể tích; diện tích S xung xung quanh và diện tích S toàn phần của hình chóp cụt này

Lời giải

Từ hình vẽ, tớ thấy

• Đường kính lòng nhỏ là d₁ = 40 centimet => nửa đường kính lòng nhỏ ${r_1} = \frac{{{d_1}}}{2} = \frac{{40}}{2} = 20\left( {cm} \right)$
• Đường kính lòng rộng lớn là d₂ = 50 centimet => nửa đường kính lòng rộng lớn ${r_2} = \frac{{{d_2}}}{2} = \frac{{50}}{2} = 25\left( {cm} \right)$
• Chiểu cao của hình h = 6 m.

Dựa vô công thức tính thể tích của hình chóp cụt phía trên, tớ thay cho số vào

$\begin{array}{l} V = \frac{{\pi h}}{3}\left( {r_1^2 + r_2^2 + {r_1}{r_2}} \right)\\ \,\,\,\,\,\, = \frac{{\pi .6}}{3}\left( {{{20}^2} + {{25}^2} + đôi mươi.25} \right)\\ \,\,\,\,\,\, = 9581,857592\left( {{m^3}} \right) \end{array}$

Mặt không giống, lúc biết lối sinh ℓ = 10 thì tớ tính được

• Diện tích xung quanh: S_xq = π.(r₁ + r₂).ℓ = π.(20 + 25).10 = 1413,716694 (m²)
• Diện tích toàn phần:

\[\begin{array}{l} {S_{tp}} = \pi \left( {r_1^2 + r_2^2 + \left( {{r_1} + {r_2}} \right).\ell } \right)\\ \,\,\,\,\,\,\, = \pi \left[ {{{20}^2} + {{25}^2} + \left( {20 + 25} \right).10} \right]\\ \,\,\,\,\,\,\, = 4633,849164\left( {{m^2}} \right) \end{array}\]

Bài tập dượt 2. Một nút chai thủy tinh nghịch là 1 trong khối tròn trặn xoay (H), một phía phẳng lặng chứa chấp trục của (H) hạn chế (H) theo dõi một tiết diện như vô hình vẽ mặt mũi. Tính thể tích của (H) (đơn vị cm³).

A. ${{V}_{\left( H \right)}}=23\pi $.

B. ${{V}_{\left( H \right)}}=13\pi $.

C. ${{V}_{\left( H \right)}}=\frac{41\pi }{3}$.

D. ${{V}_{\left( H \right)}}=17\pi $.

Hướng dẫn giải

Chọn đáp án C.

Thể tích khối trụ là V_tru=Bh=π.1,5².4=9π. Thể tích khối nón là ${{V}_{non}}=\frac{1}{3}\pi {{2}^{2}}.4=\frac{16\pi }{3}$.

Thể tích phần phú là: ${{V}_{p.giao}}=\frac{1}{3}\pi {{1}^{2}}.2=\frac{2\pi }{3}$. Vậy ${{V}_{\left( H \right)}}=9\pi +\frac{16\pi }{3}-\frac{2\pi }{3}=\frac{41\pi }{3}$.

Bài tập dượt 3. Cho nhì hình vuông vắn với nằm trong cạnh vày 5 được xếp ông chồng lên nhau sao mang lại đỉnh X của một hình vuông vắn là tâm của hình vuông vắn sót lại (như hình vẽ). Tính thể tích V của vật thể tròn trặn xoay Khi tảo quy mô bên trên xung xung quanh trục XY.

A. $V=\frac{125\left( 1+\sqrt{2} \right)\pi }{6}$.

B. $V=\frac{125\left( 5+2\sqrt{2} \right)\pi }{12}$.

C. $V=\frac{125\left( 5+4\sqrt{2} \right)\pi }{24}$.

Xem thêm: game nhiều người chơi nhất

D. $V=\frac{125\left( 2+\sqrt{2} \right)\pi }{4}$.

Hướng dẫn giải

Chọn C.

Cách 1 

Khối tròn trặn xoay bao gồm 3 phần:

Phần 1: khối trụ với độ cao vày 5, nửa đường kính lòng vày $\frac{5}{2}$ hoàn toàn có thể tích ${{V}_{1}}=\pi \times {{\left( \frac{5}{2} \right)}^{2}}\times 5=\frac{125\pi }{4}$.

Phần 2: khối nón với độ cao và nửa đường kính lòng vày $\frac{5\sqrt{2}}{2}$ hoàn toàn có thể tích

${{V}_{2}}=\frac{1}{3}\times \pi \times {{\left( \frac{5\sqrt{2}}{2} \right)}^{2}}\times \frac{5\sqrt{2}}{2}=\frac{125\pi \sqrt{2}}{12}$

Phần 3: khối nón cụt hoàn toàn có thể tích là

${{V}_{3}}=\frac{1}{3}\pi \times \frac{5\left( \sqrt{2}-1 \right)}{2}\times \left( {{\left( \frac{5\sqrt{2}}{2} \right)}^{2}}+{{\left( \frac{5}{2} \right)}^{2}}+\frac{5\sqrt{2}}{2}\times \frac{5}{2} \right)=\frac{125\left( 2\sqrt{2}-1 \right)\pi }{24}$.

Vậy thể tích khối tròn trặn xoay là

$V={{V}_{1}}+{{V}_{2}}+{{V}_{3}}=\frac{125\pi }{4}+\frac{125\pi \sqrt{2}}{12}+\frac{125\left( 2\sqrt{2}-1 \right)\pi }{24}=\frac{125\left( 5+4\sqrt{2} \right)\pi }{24}$.

Cách 2 :

Thể tích hình trụ được tạo nên trở thành kể từ hình vuông vắn $ABCD$ là ${{V}_{T}}=\pi {{R}^{2}}h=\frac{125\pi }{4}$

Thể tích khối tròn trặn xoay được tạo nên trở thành kể từ hình vuông vắn $XEYF$ là ${{V}_{2N}}=\frac{2}{3}\pi {{R}^{2}}h=\frac{125\pi \sqrt{2}}{6}$

Thể tích khối tròn trặn xoay được tạo nên trở thành kể từ tam giác $XDC$ là ${{V}_{{{N}’}}}=\frac{1}{3}\pi {{R}^{2}}h=\frac{125\pi }{24}$

Thể tích cần thiết lần $V={{V}_{T}}+{{V}_{2N}}-{{V}_{{{N}’}}}=125\pi \frac{5+4\sqrt{2}}{24}$.

Bài tập dượt 4. Một loại phễu với hình trạng nón. Người tớ sập một lượng nước vô phễu sao mang lại độ cao của lượng nước vô phễu vày $\frac{1}{3}$ độ cao của phễu. Hỏi nếu như bịt kín mồm phễu rồi lộn ngược phễu lên thì độ cao của nước vày từng nào ? hiểu rằng độ cao của phễu là $15cm$

A.$0,188\left( centimet \right)$.

B. $0,216\left( centimet \right)$.

C. $0,3\left( centimet \right)$.

D. $0,5\,\left( centimet \right)$.

Hướng dẫn giải

– Phương pháp: Tính thể tích của phần hình nón ko chứa chấp nước, kể từ ê suy rời khỏi độ cao $h’$, độ cao của nước vày độ cao phễu trừ cút $h’$.

Công thức thể tích khối nón: $V=\frac{1}{3}\pi {{\text{R}}^{2}}.h$

– Cách giải:

Gọi nửa đường kính lòng phễu là $R$, độ cao phễu là $h=15\left( centimet \right)$, tự độ cao nước vô phễu thuở đầu vày $\frac{1}{3}h$ nên nửa đường kính lòng hình nón tạo nên do lượng nước là $\frac{1}{3}R$. Thể tích phễu và thể tích nước thứu tự là $V=\frac{1}{3}\pi {{\text{R}}^{2}}.15=5\pi {{\text{R}}^{2}}\left( c{{m}^{3}} \right)$ và ${{V}_{1}}=\frac{1}{3}\pi {{\left( \frac{R}{3} \right)}^{2}}.\frac{15}{3}=\frac{5}{27}\pi {{\text{R}}^{2}}\left( c{{m}^{3}} \right)$. Suy rời khỏi thể tích phần khối nón ko chứa chấp nước là ${{V}_{2}}=V-{{V}_{1}}=5\pi {{\text{R}}^{2}}-\frac{5}{27}\pi {{\text{R}}^{2}}=\frac{130}{27}\pi {{\text{R}}^{2}}\left( c{{m}^{3}} \right)$

$\Rightarrow \frac{{{V}_{2}}}{V}=\frac{26}{27}\left( 1 \right)$. Gọi $h’$ và $r$là độ cao và nửa đường kính lòng của khối nón ko chứa chấp nước, có

Xem thêm: cuối tuần này thì sao

$\frac{h’}{h}=\frac{r}{R}\Rightarrow \frac{{{V}_{2}}}{V}=\frac{h{{‘}^{3}}}{{{h}^{3}}}=\frac{h{{‘}^{3}}}{{{15}^{3}}}\left( 2 \right)$

Từ (1) và (2) suy rời khỏi $h’=5\sqrt[3]{26}\Rightarrow {{h}_{1}}=15-5\sqrt[3]{26}\approx 0,188\left( centimet \right)$

Mục bài bác tập dượt cũng phần kết của nội dung bài viết share về chủ thể hình nón cụt. Hy vọng những share kỹ năng về công thức tính thể tích, diện tích S xung xung quanh và diện tích S toàn phần của hình nón cụt này tiếp tục khiến cho bạn hiểu thêm 1 hình trạng học tập thịnh hành, khiến cho bạn mến học tập toán rộng lớn. Trong khi, chúng ta cũng có thể tìm hiểu thêm chủ thể hình nón và đã được biên soạn khá công. Chúc bạn làm việc tập dượt hiệu suất cao.