Đường khoảng cuả tam giác là đoạn thằng nối trung điểm nhì cạnh của tam giác.
1. Kiến thức cần thiết nhớ
Đường khoảng của tam giác
![]()
Định nghĩa: Đường khoảng của tam giác là đoạn trực tiếp nối trung điểm nhì cạnh của tam giác.
Định lý 1: Đường trực tiếp trải qua trung điểm một cạnh của tam giác và tuy vậy song với cạnh loại nhì thì trải qua trung điểm cạnh loại phụ vương.
Định lý 2: Đường khoảng của tam giác thì tuy vậy song với cạnh loại phụ vương và bởi vì nửa cạnh ấy.
Ví dụ:
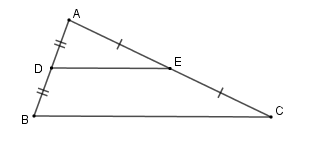
+ \(\Delta ABC\) với \(D\) là trung điểm của \(AB\) , \(E\) là trung điểm của \(AC\) nên \(DE\) là đường trung bình của tam giác \(ABC\) \( \Rightarrow DE{\rm{//}}BC;\,DE = \dfrac{1}{2}BC.\)
+ Nếu \(\left\{ \begin{array}{l}DA = DB\\DE{\rm{//}}BC\end{array} \right. \Rightarrow EC = EA\) .
Đường khoảng của hình thang
![]()
Định nghĩa: Đường khoảng của hình thang là đoạn trực tiếp nối trung điểm nhì cạnh mặt mũi của hình thang.
Định lí 3: Đường trực tiếp trải qua trung điểm một cạnh mặt mũi của hình thang và tuy vậy song với nhì lòng thì trải qua trung điểm cạnh mặt mũi loại nhì.
Định lí 4: Đường khoảng của hình thang thì tuy vậy song với nhì lòng và bởi vì nửa tổng nhì lòng.
Ví dụ:
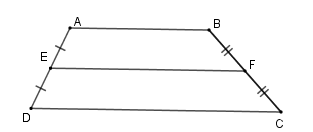
+ Hình thang \(ABCD\) (hình vẽ) với \(E\) là trung điểm \(AD\) , \(F\) là trung điểm của \(BC\) nên \(EF\) là lối khoảng của hình thang \( \Rightarrow \left\{ \begin{array}{l}EF{\rm{//}}DC\\EF = \dfrac{{AB + DC}}{2}\end{array} \right.\)
2. Các dạng toán thông thường gặp
Dạng 1: Chứng minh những hệ thức về cạnh và góc. Tính những cạnh và góc.
Phương pháp:
Xem thêm: trịnh công sơn mỗi ngày tôi chọn một niềm vui
Sử dụng đặc thù đường trung bình của tam giác và hình thang.
+ Đường khoảng của tam giác thì tuy vậy song với cạnh loại phụ vương và bởi vì nửa cạnh ấy.
+ Đường khoảng của hình thang thì tuy vậy song với nhì lòng và bởi vì nửa tổng nhì lòng.
+ Đường trực tiếp trải qua trung điểm một cạnh của tam giác và tuy vậy song với cạnh loại nhì thì trải qua trung điểm cạnh loại phụ vương.
+ Đường trực tiếp trải qua trung điểm một cạnh mặt mũi của hình thang và tuy vậy song với nhì lòng thì trải qua trung điểm cạnh mặt mũi loại nhì.
Dạng 2: Chứng minh một cạnh là đường trung bình của tam giác, hình thang.
Phương pháp:
Sử dụng khái niệm đường trung bình của tam giác và hình thang.
+ Đường khoảng của tam giác là đoạn trực tiếp nối trung điểm nhì cạnh của tam giác.
+ Đường khoảng của hình thang là đoạn trực tiếp nối trung điểm nhì cạnh mặt mũi của hình thang.

![]() Chia sẻ
Chia sẻ
-
Trả câu nói. thắc mắc 1 Bài 4 trang 76 SGK Toán 8 Tập 1
Trả câu nói. thắc mắc 1 Bài 4 trang 76 SGK Toán 8 Tập 1. Vẽ tam giác ABC bất kì rồi lấy trung điểm D của AB
-
Trả câu nói. thắc mắc 2 Bài 4 trang 77 SGK Toán 8 Tập 1
Trả câu nói. thắc mắc 2 Bài 4 trang 77 SGK Toán 8 Tập 1. Vẽ tam giác ABC bất kì rồi lấy trung điểm D
-
Trả câu nói. thắc mắc 3 Bài 4 trang 77 SGK Toán 8 Tập 1
Trả câu nói. thắc mắc 3 Bài 4 trang 77 SGK Toán 8 Tập 1. Tính phỏng nhiều năm đoạn BC bên trên hình 33.
-
Trả câu nói. thắc mắc 4 Bài 4 trang 78 SGK Toán 8 Tập 1
Cho hình thang ABCD (AB // CD). Qua trung điểm E của AD kẻ đường thẳng liền mạch tuy vậy song với nhì lòng, đường thẳng liền mạch này tách AC ở I, tách BC ở F (h.37)...
-
Trả câu nói. thắc mắc 5 Bài 4 trang 79 SGK Toán 8 Tập 1
Tìm x bên trên hình 40
>> Xem thêm
Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay
Xem thêm: ngày xưa tôi có quen một người em gái nhỏ
Tham Gia Group Dành Cho 2K10 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

>> Học trực tuyến lớp 8 bên trên Tuyensinh247.com khẳng định chung học viên lớp 8 học tập đảm bảo chất lượng, trả trả tiền học phí nếu như học tập ko hiệu suất cao.










Bình luận