nghiệm của phương trình bậc 2

Phương trình bậc 2 là 1 kỹ năng và kiến thức cơ phiên bản tuy nhiên nhiều bạn và đã được học tập kể từ thời cấp cho 2. Từ những lý lẽ cơ phiên bản cho tới những phần mềm phức tạp, phương trình bậc 2 không chỉ là là 1 định nghĩa toán học tập trừu tượng, mà còn phải đem nhập bản thân những độ quý hiếm thực tiễn biệt vô nằm trong cần thiết. Nhưng các bạn từng tự động căn vặn cơ hội giải phương trình bậc 2 là gì và tại vì sao này lại được dùng thịnh hành cho tới vậy? Trong nội dung bài viết này, tất cả chúng ta tiếp tục cùng với nhau tò mò cách thức mò mẫm nghiệm phương trình bậc 2 kể từ những kỹ năng và kiến thức cơ phiên bản cho tới phần mềm thực tiễn biệt.

Định nghĩa cơ phiên bản của phương trình bậc 2

Phương trình bậc 2 là 1 loại phương trình toán học tập đem dạng đặc biệt quan trọng, nhập bại liệt đem một số trong những hằng số và một trở thành số đem số nón là 2. Dạng phương trình này hoàn toàn có thể trình diễn những mối liên hệ Một trong những trở thành số trong không ít nghành nghề không giống nhau như vật lý cơ, nghệ thuật, tài chính, khoa học tập ngẫu nhiên,… Phương trình bậc 2 cũng là 1 dụng cụ cần thiết trong công việc phân tích những hàm số đem dạng tương tự động, đàng cong đem hình chữ U, quyết định lý về tam giác vuông và nhiều định nghĩa toán học tập không giống.

Bạn đang xem: nghiệm của phương trình bậc 2

Hiểu được cách thức giải phương trình bậc 2 không chỉ là giúp cho bạn nắm rõ kỹ năng và kiến thức toán học tập cơ phiên bản, tuy nhiên còn hỗ trợ các bạn vận dụng nhập những Việc thực tiễn nhập cuộc sống đời thường hằng ngày. quý khách hàng hoàn toàn có thể sử dụng phương trình bậc 2 nhằm đo lường ngân sách, lợi tức đầu tư, diện tích S, thể tích, khoảng cách, vận tốc,… quý khách hàng cũng hoàn toàn có thể sử dụng kỹ năng và kiến thức của phương trình này nhằm quy mô hóa những hiện tượng kỳ lạ ngẫu nhiên như sự biến hóa nhiệt độ chừng, chừng cao, áp suất,…

Bằng những cách thức mò mẫm nghiệm phương trình bậc 2, chúng ta có thể mò mẫm đi ra những nghiệm hoặc những độ quý hiếm của trở thành số thỏa mãn nhu cầu phương trình. Từ bại liệt suy đi ra những tóm lại hoặc lý giải cho những Việc không giống nhau. Tuy nhiên tùy vào cụ thể từng tình huống tuy nhiên chúng ta có thể vận dụng những cách thức không giống nhau.

Phương trình bậc 2 là 1 trong mỗi định nghĩa cơ phiên bản nhập toán học tập và việc giải phương trình này hoàn toàn có thể tạo ra trở ngại so với nhiều người. Trên thực tiễn, mang trong mình một cơ hội mò mẫm nghiệm phương trình bậc 2 giản dị nhất tuy nhiên chúng ta có thể vận dụng. Với chỉ dẫn tại đây, tất cả chúng ta tiếp tục tò mò tiến độ mò mẫm nghiệm của phương trình này một cơ hội đơn giản và dễ dàng và hiệu suất cao.

Sử dụng công thức nghiệm nhằm tính phương trình bậc 2

Công thức nghiệm của phương trình bậc 2 là 1 công thức toán học tập cần thiết gom tất cả chúng ta mò mẫm đi ra những độ quý hiếm nghiệm của phương trình. Công thức này tùy thuộc vào những hằng số a, b và c nhập phương trình bậc 2. Công thức nghiệm đem dạng: x = (−b ± √(b^2 – 4ac))/(2a).

Để ghi nhớ công thức nghiệm này và giải phương trình bậc 2, chúng ta có thể dùng một số trong những cơ hội ghi nhớ giản dị. Một cơ hội là ghi ghi nhớ những ký tự động nhập công thức và để ý quan hệ đằm thắm bọn chúng.

Ví dụ, nhập công thức nghiệm, tớ đem những ký tự động a, b, c, ±, √, ^2, -, 4 và 2. quý khách hàng hoàn toàn có thể tưởng tượng rằng “a” đứng bên trên đỉnh và “b” và “c” ở bên dưới. Dấu “+/-” thể hiện nay sự lựa lựa chọn đằm thắm vết nằm trong và vết trừ Lúc đo lường. Dấu “√” biểu thị căn bậc nhì, “b^2” là bình phương của b, còn “4ac” là tích của 4, a và c. phẳng cơ hội ghi ghi nhớ và link những ký tự động này, chúng ta có thể đơn giản và dễ dàng ghi nhớ công thức nghiệm.

Một cách thứ hai nhằm ghi ghi nhớ công thức nghiệm là học tập nằm trong một câu thơ ghi nhớ. Ta đem câu thơ “Bé loại bỏ đi, bình phương trừ tứ a nằm trong, Hai a phân chia, căn bậc nhì nằm trong trừ” hoàn toàn có thể giúp cho bạn ghi nhớ quá trình đo lường nhập công thức nghiệm. Câu thơ này theo thứ tự nói đến việc quăng quật vết trừ, tính bình phương của b và trừ lên đường 4ac, tiếp sau đó phân chia mang lại 2a và sau cùng tính căn bậc nhì và nằm trong hoặc trừ.

Tính toán và lý giải quy trình vận dụng công thức nghiệm

Để vận dụng công thức nghiệm Lúc giải phương trình bậc 2, bạn phải tiến hành những thao tác sau đây:

Bước 1: Xác quyết định những hằng số a,b,c nhập phương trình bậc 2. quý khách hàng cần thiết để ý rằng a là thông số của x2 , b là thông số của x  và c là hằng số tự tại. Nếu phương trình không tồn tại 1 trong các phụ thân hằng số này, chúng ta có thể coi hằng số bại liệt bởi vì 0.

Bước 2: Thay những hằng số nhập công thức nghiệm và đo lường độ quý hiếm của biểu thức bên phía trong căn bậc nhì, gọi là biệt thức delta (Δ ). Biệt thức delta là một số trong những cần thiết, vì thế nó đưa ra quyết định số nghiệm của phương trình. Biệt thức delta đem công thức là Δ=b2−4ac.

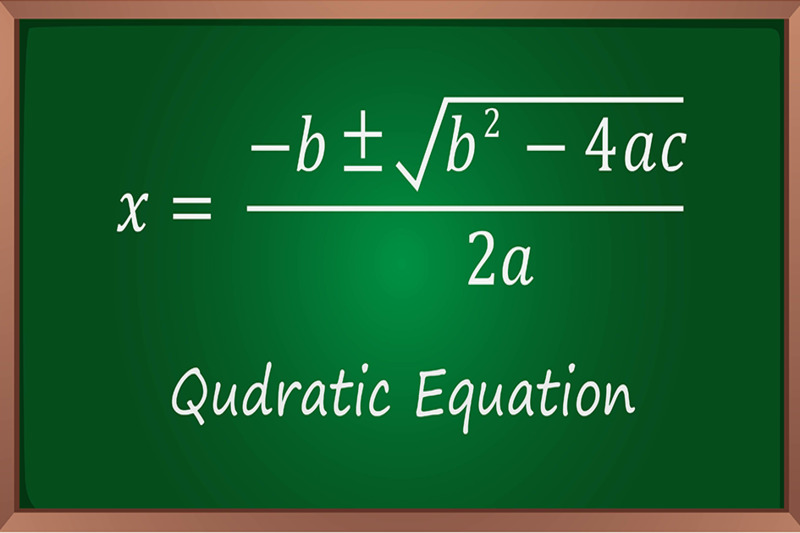
Bước 3: Kiểm tra độ quý hiếm của biệt thức Delta nhằm xác lập số nghiệm của phương trình.

• Trong tình huống Δ>0 thì phương trình sẽ có được nhì nghiệm phân biệt.
• Nếu Δ=0, phương trình đem nghiệm kép. Còn nếu như Δ<0 thì phương trình tiếp tục vô nghiệm.
• Nếu biệt thức delta là một số trong những âm, các bạn ko thể lấy căn bậc nhì của chính nó. Vì nhập tình huống này phương trình không tồn tại nghiệm thực.

Bước 4: Tính toán độ quý hiếm của những nghiệm bằng phương pháp thay cho độ quý hiếm của biệt thức Delta nhập công thức nghiệm và thực hiện tròn trặn thành phẩm nếu như cần thiết. Hãy để ý rằng công thức nghiệm đem nhì vết cộng/trừ (±). Vì vậy cần thiết đo lường nhì độ quý hiếm của x với nhì vết này. quý khách hàng cũng cần được để ý rằng nếu như biệt thức Delta bởi vì 0, các bạn chỉ việc đo lường một độ quý hiếm của x, vì thế nhì nghiệm trùng nhau.

Một số cách thức giải phương trình bậc 2 khác

Ngoài cơ hội mò mẫm nghiệm phương trình bậc 2 giản dị nhất tuy nhiên tất cả chúng ta tiếp tục tò mò phía trên, còn tồn bên trên một số trong những cách thức không giống hoàn toàn có thể giải quyết và xử lý những phương trình này. Tùy nằm trong nhập dạng và điểm lưu ý của phương trình tuy nhiên chúng ta có thể lựa lựa chọn cách thức thích hợp nhất nhằm giải được Việc.

Xem thêm: mẫu bản kiểm điểm cá nhân

Xem xét những tình huống đặc biệt quan trọng Lúc giải phương trình bậc 2

Trong quy trình mò mẫm nghiệm phương trình bậc 2, tất cả chúng ta cần thiết đánh giá những tình huống đặc biệt quan trọng nhằm phân biệt nghiệm một cơ hội nhanh gọn và hiệu suất cao. Dưới đó là một số trong những tình huống đặc biệt quan trọng xứng đáng để ý Lúc giải loại phương trình này:

Phương trình vô nghiệm: Trường thích hợp này xẩy ra Lúc những thông số a, b, c đều nằm trong vết và độ quý hiếm vô cùng của a nhỏ rộng lớn độ quý hiếm vô cùng của c. Ví dụ: x2+2x+3=0 là 1 phương trình vô nghiệm. Trong tình huống này, vì thế a, b, c đều dương và ∣a∣<∣c∣ nên phương trình không tồn tại nghiệm thực.

Phương trình đem vô số nghiệm: Trường thích hợp này xẩy ra Lúc toàn bộ những thông số a, b, c đều bởi vì 0. Ví dụ: 0x2+0x+0=0 là 1 phương trình đem vô số nghiệm. Trong tình huống này thì từng độ quý hiếm của x đều là nghiệm của phương trình.

Phương trình đem nghiệm kép: Trường thích hợp này xẩy ra Lúc những thông số a, b, c thỏa mãn nhu cầu 1 trong các nhì điều kiện: a+b+c=0 hoặc a−b+c=0. Ví dụ: x2−5x+6=0 đem nghiệm kép x=3. Trong tình huống này thì phương trình có được chỉ tồn tại một nghiệm độc nhất.

Việc phân biệt và xử lý những tình huống đặc biệt quan trọng này gom tất cả chúng ta tiết kiệm chi phí thời hạn và nỗ lực nhập quy trình mò mẫm nghiệm phương trình bậc 2. Tuy nhiên, lúc không thỏa mãn nhu cầu những tình huống đặc biệt quan trọng, tất cả chúng ta vẫn hoàn toàn có thể dùng công thức nghiệm nhằm mò mẫm đi ra những độ quý hiếm của x một cơ hội cụ thể và đúng đắn.

Phương pháp đồ dùng thị nhằm giải phương trình bậc 2

Phương pháp đồ dùng thị là 1 trong mỗi cơ hội tiếp cận thịnh hành nhằm giải quyết và xử lý những Việc tương quan cho tới phương trình bậc 2. Để vận dụng cách thức này, tớ nên biết kiểu vẽ đồ dùng thị của hàm số y=ax^2+bx+c, nhập bại liệt a, b, c là những thông số mang lại trước. Đồ thị của hàm số này còn có dạng một Parabol (hay thường hay gọi là đàng cong U), mang trong mình một điểm cực kỳ trị là đỉnh của Parabol.

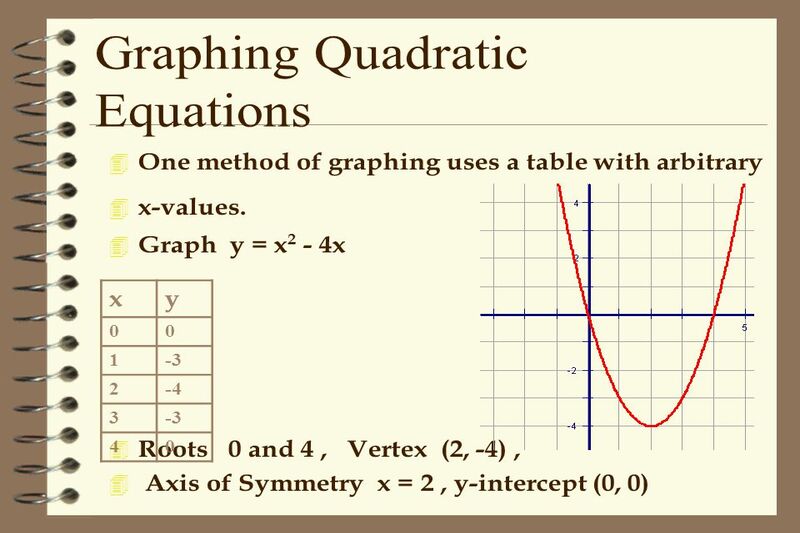
Khi vẽ đồ dùng thị, tớ cần thiết để ý cho tới những nhân tố sau: Độ dốc, phía banh, tâm đối xứng và phó điểm với những trục tọa chừng. Các phó điểm của đồ dùng thị với trục hoành là những độ quý hiếm của x thỏa mãn nhu cầu phương trình y=0 hoặc thưa cách thứ hai là những nghiệm của phương trình bậc 2.

Phương pháp đồ dùng thị chất lượng tốt thế là đỡ đần ta đem ánh nhìn tổng quát tháo và sống động về thực chất của phương trình bậc 2, giống như năng lực đối chiếu và phân loại những tình huống đem nghiệm, vô nghiệm hoặc đem nghiệm kép. Tuy nhiên, cách thức này cũng gặp gỡ cần một số trong những giới hạn như sai số tự quy trình vẽ đồ dùng thị ko thể trọn vẹn đúng đắn, tùy thuộc vào tài năng và dụng cụ vẽ đồ dùng thị của những người giải và trở ngại trong công việc xác lập nghiệm đúng đắn. Những trở ngại này hoặc xẩy ra Lúc đồ dùng thị hạn chế trục hoành ở những điểm đem tọa chừng là những số thập phân, phân số hoặc số căn.

Phương pháp nhẩm nghiệm

Đây là cách thức giải phương trình bậc 2 dựa vào việc phân biệt một số trong những dạng đặc biệt quan trọng của phương trình bậc 2. Nó được vận dụng theo đòi một quyết định lý không xa lạ, bại liệt đó là quyết định lý Vi-et. Phương pháp nghiệm là 1 cách thức nhẩm nhanh chóng được nghiệm tuy nhiên ko cần dùng công thức nghiệm. Một số dạng phương trình bậc 2 hoàn toàn có thể nhẩm nghiệm như sau:

Phương trình đem dạng ax^2 + bx + c = 0 với a + b + c = 0. Phương trình này sẽ có được nghiệm x1 = 1 và x2 = c/a.

Phương trình đem dạng ax^2 + bx + c = 0 với a – b + c = 0. Phương trình này sẽ có được nghiệm x1 = -1 và x2 = -c/a.

Phương trình đem dạng ax^2 + (a + b)x + b = 0. Phương trình này sẽ có được nghiệm x1 = -1 và x2 = -b/a.

Phương trình đem dạng x^2 + px + q = 0 với p, q là những số nguyên vẹn và q phân chia không còn mang lại p. Phương trình này sẽ có được nghiệm x1 = -p và x2 = -q/p.

Xem thêm: Kèo chấp là gì? Kinh nghiệm cá cược Kèo chấp  bất bại 2024

Phương pháp nhẩm nghiệm đỡ đần ta giải phương trình bậc 2 một cơ hội nhanh gọn và thuận tiện Lúc những dạng đặc biệt quan trọng của phương trình được phân biệt và vận dụng. Tuy nhiên, nó chỉ vận dụng được mang lại một số trong những dạng ví dụ của phương trình và ko thể dùng mang lại toàn bộ những tình huống.

Kết luận

Trong nội dung bài viết này, tất cả chúng ta tiếp tục mò mẫm hiểu về phương trình bậc 2 và cơ hội giải phương trình này. Đây là những kỹ năng và kiến thức cơ phiên bản và cần thiết trong công việc học tập toán học tập. phẳng cơ hội nắm rõ những công thức và cách thức giải phương trình bậc 2, tất cả chúng ta hoàn toàn có thể giải quyết và xử lý những Việc tương quan cho tới phương trình bậc 2 một cách  nhanh gọn và giản dị nhất. Hy vọng nội dung bài viết này sẽ hỗ trợ ích mang lại chúng ta trong công việc tiếp thu kiến thức và bổ sung cập nhật thêm thắt kỹ năng và kiến thức.

Xem thêm:

• Dấu hiệu phân biệt tứ giác nội tiếp và ví dụ minh hoạ
• C++ là gì? Tổng thích hợp kỹ năng và kiến thức học tập C++ cơ phiên bản cực kỳ dễ dàng hiểu