hai tam giác đồng dạng

By Admin 09/04/2024 0

1. Định nghĩa Tam giác A'B'C' gọi là đồng dạng với tam giác ABC nếu:

I. Các kỹ năng cần thiết nhớ

Bạn đang xem: hai tam giác đồng dạng

Định nghĩa:

Hai tam giác gọi là đồng dạng cùng nhau nếu như bọn chúng đem phụ thân cặp góc đều nhau từng song một và phụ thân cặp cạnh ứng tỉ lệ thành phần.

Ví dụ: $\Delta ABC$ $\backsim$ $\Delta A'B'C'$\( \Leftrightarrow \left\{ \begin{array}{l}\widehat A = \widehat {A'},\,\widehat B = \widehat {B'},\widehat C = \widehat {C'}\\\dfrac{{AB}}{{A'B'}} = \dfrac{{BC}}{{B'C'}} = \dfrac{{CA}}{{C'A'}}\end{array} \right.\)

Chú ý: 

* Tỉ số những cạnh ứng \(\dfrac{{AB}}{{A'B'}} = \dfrac{{BC}}{{B'C'}} = \dfrac{{CA}}{{C'A'}} = k\) được gọi là tỉ số đồng dạng  của nhì tam giác.

Định lí về dẫn đến hai tam giác đồng dạng

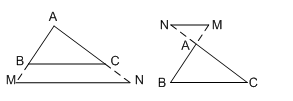
Nếu một đường thẳng liền mạch tách nhì cạnh của tam giác và tuy nhiên song với cạnh sót lại thì  nó tạo ra trở nên một tam giác mới nhất đồng dạng với tam giác đang được mang đến.

Cho $\Delta ABC$, $MN{\rm{//}}BC$

$ \Rightarrow \Delta AMN$$\backsim$$\Delta ABC.$

Chú ý: Định lí cũng giống nhập tình huống đường thẳng liền mạch tách phần kéo dãn dài nhì cạnh của tam giác và tuy nhiên song với cạnh sót lại.

II. Các dạng toán thông thường gặp

Dạng 1: Sử dụng tam giác đồng dạng nhằm tính phỏng nhiều năm cạnh, chu vi, tỉ số đồng dạng, số đo góc…

Phương pháp:

Xem thêm: cách bật nút home ảo trên iphone

Ta dùng khái niệm và tấp tểnh lý về hai tam giác đồng dạng. Sử dụng tấp tểnh lý Ta-lét và đặc thù tỉ lệ thành phần thức nhằm đo lường.

$\Delta ABC$ $\backsim$ $\Delta A'B'C'$\( \Leftrightarrow \left\{ \begin{array}{l}\widehat A = \widehat {A'},\,\widehat B = \widehat {B'},\widehat C = \widehat {C'}\\\dfrac{{AB}}{{A'B'}} = \dfrac{{BC}}{{B'C'}} = \dfrac{{CA}}{{C'A'}}\end{array} \right.\)

Dạng 2: Sử dụng tam giác đồng dạng nhằm chứng tỏ những nguyên tố hình học tập (hai đường thẳng liền mạch tuy nhiên tuy nhiên, …)

Phương pháp:

Ta dùng $\Delta ABC$ $\backsim$ $\Delta A'B'C'$\( \Leftrightarrow \left\{ \begin{array}{l}\widehat A = \widehat {A'},\,\widehat B = \widehat {B'},\widehat C = \widehat {C'}\\\dfrac{{AB}}{{A'B'}} = \dfrac{{BC}}{{B'C'}} = \dfrac{{CA}}{{C'A'}}\end{array} \right.\)

Và tấp tểnh lý:  Nếu một đường thẳng liền mạch tách nhì cạnh của tam giác và tuy nhiên song với cạnh sót lại thì  nó tạo ra trở nên một tam giác mới nhất đồng dạng với tam giác đang được mang đến.


Bình luận

Chia sẻ

>> Xem thêm

Luyện Bài Tập Trắc nghiệm Toán 8 - Xem ngay

Xem thêm: em sẽ tắt máy mỗi khi nhớ người

Báo lỗi - Góp ý

Tham Gia Group Dành Cho 2K10 Chia Sẻ, Trao Đổi Tài Liệu Miễn Phí

>> Học trực tuyến lớp 9 & quãng thời gian Up 10! bên trên Tuyensinh247.com Đầy đầy đủ khoá học tập những cuốn sách (Kết nối trí thức với cuộc sống; Chân trời sáng sủa tạo; Cánh diều), theo đuổi quãng thời gian 3 bước: Nền Tảng, Luyện Thi, Luyện Đề. rứt phá huỷ điểm lớp 9, thi đua nhập lớp 10 thành phẩm cao. Hoàn trả chi phí khóa học nếu như học tập ko hiệu suất cao.