Hãy nhập thắc mắc của khách hàng vô phía trên, nếu như là thông tin tài khoản VIP, các bạn sẽ được ưu tiên vấn đáp.
- Tất cả
- Câu căn vặn hay
- Chưa trả lời
- Câu căn vặn vip

Bạn đang xem: cho tam giác abc cân tại a
a, Xét tam giác ADB và tam giác AEC với :
AE = AD ( gt )
\(\widehat{A}\) chung
AB = AC ( gt )
=> \(\Delta ADB=\Delta AEC\left(c-g-c\right)\)
b, Do \(\Delta ADB=\Delta AEC\) ( câu a, )
=> \(\widehat{ABD}=\widehat{ACE}\) ( 2 góc ứng )
BD nằm trong lòng 2 tia EB và EC
=> \(\widehat{EBD}+\widehat{CBD}=\widehat{B}\)
\(\Rightarrow\widehat{CBD}=\widehat{B}-\widehat{EBD}\) ( 1 )
CE nằm trong lòng 2 tia CD và CB
\(\Rightarrow\widehat{BCE}+\widehat{DCE}=\widehat{C}\)
\(\Rightarrow\widehat{BCE}=\widehat{C}-\widehat{DCE}\) ( 2 )
Từ ( 1 ) và ( 2 )
=> \(\widehat{CBD}=\widehat{BCE}\) hay \(\widehat{IBC}=\widehat{ICB}\)
Xét tam giác IBC có
\(\widehat{IBC}=\widehat{ICB}\)
=> tam giác IBC cân nặng bên trên I
c, Xét tam giác AED với :
AE = AD ( gt )
=> Tam giác AED cân nặng bên trên A
=> \(\widehat{AED}=\dfrac{180^0-\widehat{A}}{2}\)( 3 )
Tam giác ABC cân nặng bên trên A
=> \(\widehat{B}=\dfrac{180^0-\widehat{A}}{2}\) ( 4 )
Từ ( 3 ) , ( 4) => \(\widehat{AED}=\widehat{B}\)
Đường trực tiếp AB bị 2 đường thẳng liền mạch ED và BC tách tạo ra trở nên cặp góc đồng vị vì chưng nhau \(\widehat{AED}=\widehat{B}\)
=> ED // BC ( đpcm)


`a)`
Có `Delta ABC ` cân nặng bên trên `A(GT)=>AB=AC`
Xét `Delta ADB` và `Delta AEC` có:
`{:(AB=AC(cmt)),(hat(A)-chung),(AD=AE(GT)):}}`
`=>Delta ADB=Delta AEC(c.g.c)(đpcm)`
`b)`
Có `Delta ABC` cân nặng bên trên `A=>hat(ABC)=hat(ACB)`
`=>hat(EBC)=hat(DCB)`
mà `hat(B_1)=hat(C_1)(Delta ADB=Delta AEC)`
`hat(B_1)+hat(B_2)=hat(EBC)`
`hat(C_1)+hat(C_2)=hat(DCB)`
nên `hat(B_2)=hat(C_2)`
`=>Delta IBC` cân nặng bên trên `I`
`c)`
Có `AE=AD(GT)=>Delta AED` cân nặng bên trên `A`
`=>hat(E_1)=(180^0-hat(A))/2(1)`
`Delta ABC` cân nặng bên trên `A(GT)=>hat(ABC)=(180^0-hat(A))/2(2)`
Từ `(1)` và `(2)=>hat(E_1)=hat(ABC)`
mà `2` góc này ở địa điểm đ/vị
nên `ED////BC(đpcm)`
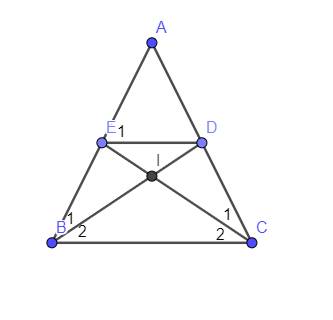

a, Vì \(\left\{{}\begin{matrix}AB=AC\\AD=AE\\\widehat{BAC}.chung\end{matrix}\right.\) nên \(\Delta ABD=\Delta ACE\left(c.g.c\right)\)
b, Vì \(\Delta ABD=\Delta ACE\) nên \(\widehat{ABD}=\widehat{ACE}\)
Mà \(\widehat{ABC}=\widehat{ACB}\) nên \(\widehat{ABC}-\widehat{ABD}=\widehat{ACB}-\widehat{ACE}\)
Do đó \(\widehat{IBC}=\widehat{ICB}\) nên tam giác IBC cân nặng bên trên I
c, \(AD=AE\) nên tg ADE cân nặng bên trên A
Do đó \(\widehat{AED}=\dfrac{180^0-\widehat{BAC}}{2}\)
Mà tg ABC cân nặng bên trên A nên \(\widehat{ABC}=\dfrac{180^0-\widehat{BAC}}{2}\)
\(\Rightarrow\widehat{AED}=\widehat{ABC}\)
Mà 2 góc này ở địa điểm đồng vị nên DE//BC

a) Xét △ AED có AE=AD nến △AED cân nặng tại A
⇒\(\widehat{AED}=\widehat{ADE}\) ⇒\(\widehat{DEB}=\widehat{EDC}\)
△ABC cân ⇒AB=AC mà AE=AD⇒EB=DC
Xét △DEB và △EDC có :
\(\widehat{DEB}=\widehat{EDC}\left(cmt\right)\)
ED : cạnh chung
EB=DC \(\left(cmt\right)\)
Do đó : △DEB = △EDC \(\left(c.g.c\right)\)
Nên \(\widehat{EBD}=\widehat{DCE}\) hay \(\widehat{ABD}=\widehat{ACE}\)
b) △ABC cân ⇒\(\widehat{ABC}=\widehat{ACB}\) mà \(\widehat{ABD}=\widehat{ACE}\) (câu a) ⇒\(\widehat{IBC}=\widehat{ICB}\)
Vậy △IBC cân nặng tại I
c) Xét △AIB và △AIC có :
AB=AC(gt)
\(\widehat{ABD}=\widehat{ACE}\) (câu a)
Xem thêm: game nhiều người chơi nhất
BI=CI(vì △IBC cân nặng tại I)
Do đó :△AIB=△AIC\(\left(c.g.c\right)\)
⇒\(\widehat{BAI}=\widehat{CAI}\) ⇒ AI là tia phân giác \(\widehat{BAC}\)
d) Xét △AED và △ABC có :
A : chung
\(\dfrac{AE}{AB}=\dfrac{AD}{AC}\)
Nên △AED đồng dạng △ABC \(\left(c.g.c\right)\)
⇒\(\widehat{AED}=\widehat{ABC}\) ⇒ ED//BC
Vì AI là đường phân giác của △AED mà △AED cân nặng nên AI cũng là đường cao ⇒AI⊥ED lại có : ED//BC ⇒AI⊥BC
e) AI⊥BC (AI là đường cao tam giác ABC) mà △ABC cân nặng nên AI cũng là đường trung tuyến ⇒ AI là đường trung trực của BC
a, Xét tam giác ABD và tam giác ACE tớ với :
^A _ chung
^AB = AC ( gt )
AD = AE ( gt )
Vậy tam giác ABD = tam giác ACE ( g.c.g )
b, => ^ABD = ^ACE ( 2 góc ứng )
mà tam giác ABC cân nặng bên trên => ^B = ^C
=> ^B - ^ABD = ^DBC
=> ^C - ^ACE = ^ECB
=> ^DBC = ^ECB
Xét tam giác IBC với : ^DBC = ^ECB
nên IBC là tam giác cân nặng bên trên I
c, Xét tam giác ABI và tam giác ACI tớ với :
^ABI = ^ACI ( cmt )
AB = AC ( gt)
IA _ chung
Vậy tam giác ABI = tam giác ACI ( c.g.c )
=> ^BAI = ^CAI ( 2 góc ứng )
Vậy AI là phân giác ^BAC
d, Ta với : \(\dfrac{AE}{AB}=\dfrac{AD}{AC}\)=> ED // BC ( Ta lét hòn đảo )
mà AI là phân giác của tam giác ABC cân nặng bên trên A
=> AI đôi khi là đàng cao
=> AI vuông BC ; ED // BC (cmt)
=> AI vuông ED
e, Xét tam giác ABC cân nặng bên trên A
AI là đàng cao, phân giác
đồng thời AI là đàng trung trực đoạn BC

Câu c) với gì tê liệt sai sai chúng ta ạ
.ko biết cô cho tới đề như thế á



Tham khảo
* Tự vẽ hình nha !
a. Xét ΔABD và ΔACE ta có:
AB=AC (ΔABC cân bên trên A)
Góc A là góc công cộng.
AD=AE (gt)
=> ΔABD=ΔACE (c-g-c)
=> Góc ABD=góc ACE (2 góc tương ứng)
b. Ta có: góc ABD + góc IBC = góc ABC
góc ACE + góc ICB = góc ACB
Mà góc ABC = góc Ngân Hàng Á Châu ACB (ΔABC cân bên trên A)
góc ABD = góc ACE (cmt)
=> Góc IBC = góc ICB
=> ΔIBC cân bên trên I.
a) Xét ΔABD và ΔACE có
AB=AC(ΔABC cân nặng bên trên A)
\(\widehat{BAD}\) chung
AD=AE(gt)
Do đó: ΔABD=ΔACE(c-g-c)
Suy ra: \(\widehat{ABD}=\widehat{ACE}\)(hai góc tương ứng)
b) Ta có: AE+EB=AB(E nằm trong lòng A và B)
AD+DC=AC(D nằm trong lòng A và C)
mà AE=AD(gt)
và AB=AC(ΔABC cân nặng bên trên A)
nên EB=DC
Xét ΔEBC và ΔDCB có
EB=DC(cmt)
\(\widehat{EBC}=\widehat{DCB}\)(hai góc ở lòng của ΔBAC cân nặng bên trên A)
BC chung
Do đó: ΔEBC=ΔDCB(c-g-c)
Suy ra: \(\widehat{ECB}=\widehat{DBC}\)(hai góc tương ứng)
hay \(\widehat{IBC}=\widehat{ICB}\)
Xem thêm: vẽ con vật đơn giản cho be
Xét ΔIBC có \(\widehat{IBC}=\widehat{ICB}\)(cmt)
nên ΔIBC cân nặng bên trên I(Định nghĩa tam giác cân)












Bình luận