Chủ đề Công thức diện tích S tam giác lớp 5: Công thức diện tích S tam giác lớp 5 là 1 công thức giản dị và dễ dàng nắm bắt nhằm mục đích tính diện tích S của một hình tam giác trải qua chiều nhiều năm cạnh lòng và độ cao. Với công thức này, học viên lớp 5 rất có thể đơn giản và dễ dàng đo lường và tính toán và vận dụng vô những bài bác tập luyện vô sách giáo trình. Việc hiểu và dùng công thức này sẽ hỗ trợ học viên trở nên tân tiến khả năng toán học tập và tập luyện năng lực logic.
Cách tính diện tích S tam giác lớp 5 là gì?
Cách tính diện tích S tam giác lớp 5 là dùng công thức: Diện tích tam giác vị một nửa tích của chừng nhiều năm lòng nhân với độ cao. Công thức đúng là S = (b x h) / 2, vô bại S là diện tích S tam giác, b là chừng nhiều năm lòng và h là độ cao.
Để tính diện tích S tam giác, các bạn nên biết chừng nhiều năm lòng và độ cao của tam giác. Thứ nhất, định hình những đơn vị chức năng đo của lòng và độ cao cần bên nhau. Sau bại, triển khai quy tắc nhân thân thiết chừng nhiều năm lòng và độ cao. Cuối nằm trong, lấy sản phẩm và phân tách mang đến 2 sẽ được diện tích S tam giác. Ví dụ:
Ví dụ: Hãy tính diện tích S tam giác với lòng nhiều năm 8 centimet và độ cao 6 centimet.
S = (b x h) / 2 = (8 centimet x 6 cm) / 2 = 48 cm² / 2 = 24 cm²
Vậy diện tích S tam giác này là 24 cm².
Bạn đang xem: công thức tính diện tích tam giác lớp 5
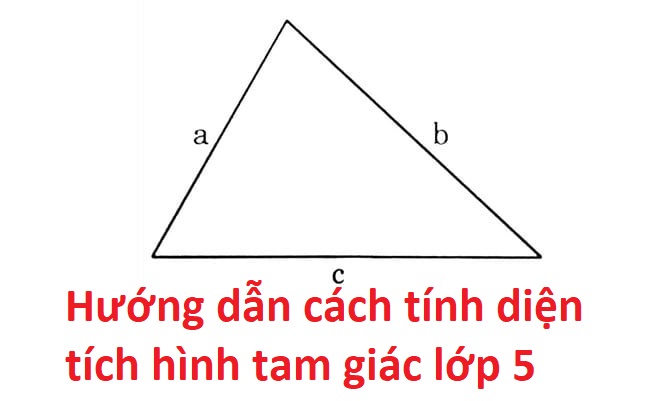
Công thức tính diện tích S tam giác là gì?
Công thức tính diện tích S tam giác là: S = (a x h) / 2.
Trong đó:
- S là diện tích S tam giác.
- a là chiều nhiều năm cạnh lòng của tam giác.
- h là độ cao của tam giác, được đo vuông góc kể từ đỉnh của tam giác xuống cạnh lòng.
Cách tính độ cao của tam giác?
Cách tính độ cao của tam giác là sử dụng công thức diện tích S của tam giác và biết diện tích S tam giác tiếp tục mang đến.
Bước 1: Gọi diện tích S tam giác là S và chiều nhiều năm cạnh lòng là a.
Bước 2: Sử dụng công thức diện tích S tam giác S = (a x h)/2 và biết độ quý hiếm S, mò mẫm độ quý hiếm của h (chiều cao).
Bước 3: Đổi công thức bên trên trở thành h = (2 x S)/a.
Bước 4: Thay độ quý hiếm của S và a vô công thức bên trên nhằm tính giá tốt trị của h.
Ví dụ: Nếu diện tích S tam giác là 15 đơn vị chức năng vuông và chiều nhiều năm cạnh lòng là 6 đơn vị chức năng, tớ rất có thể tính được độ cao bằng phương pháp thay cho độ quý hiếm vô công thức h = (2 x 15)/6 = 30/6 = 5 đơn vị chức năng. Vậy độ cao của tam giác là 5 đơn vị chức năng.
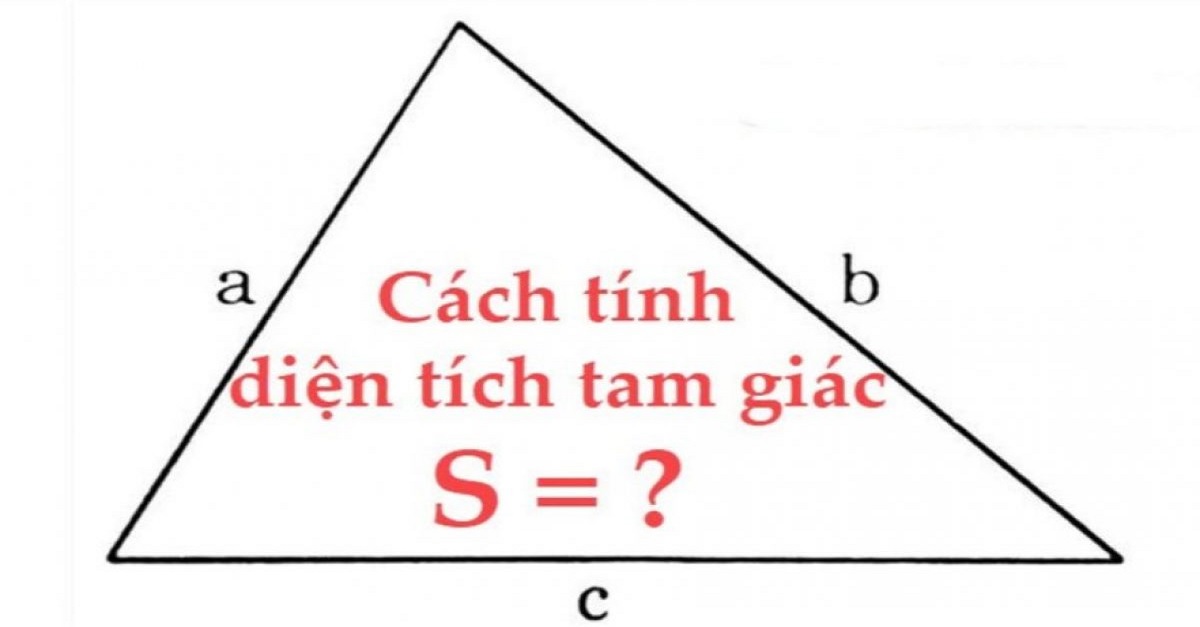
Diện tích tam giác vị từng nào phiên chiều cao?
Để tính diện tích S tam giác, tớ dùng công thức S = (a x h)/2. Trong số đó, a là chiều nhiều năm cạnh lòng của tam giác và h là độ cao ứng với cạnh lòng bại.
- Thứ nhất, tớ cần thiết xác lập chiều nhiều năm cạnh lòng và độ cao của tam giác.
- Sau bại, tớ nhân chiều nhiều năm cạnh lòng với độ cao và phân tách sản phẩm mang đến 2.
Ví dụ: Nếu tớ với tam giác với chiều nhiều năm cạnh lòng là 6cm và độ cao ứng là 4cm, tớ tính diện tích S vị cách:
S = (a x h)/2 = (6 x 4)/2 = 12 cm².
Do bại, diện tích S của tam giác này là 12cm².
Diện tích tam giác - Toán lớp 5 - Cô Phan Giang
Bạn ham muốn làm rõ rộng lớn về Diện tích tam giác và phần mềm của chính nó vô cuộc sống đời thường mặt hàng ngày? Hãy coi Clip này nhằm tò mò phương pháp tính toán diện tích S tam giác một cơ hội giản dị và thú vị.
Tại sao công thức tính diện tích S tam giác chỉ vận dụng mang đến tam giác thường?
Công thức tính diện tích S tam giác S = (a x h)/2 chỉ vận dụng mang đến tam giác thông thường vì thế tam giác thông thường với cạnh lòng và độ cao. Trong Khi bại, tam giác quan trọng như tam giác đều, tam giác vuông ko thể vận dụng công thức này vì thế bọn chúng không tồn tại cạnh lòng và/hoặc độ cao rõ nét. Công thức tính diện tích S tam giác đều, vô tình huống này, là S = (a^2 x √3)/4, vô bại a là chừng nhiều năm cạnh tam giác đều. Còn công thức tính diện tích S tam giác vuông là S = (a x b)/2, vô bại a và b theo thứ tự là chừng nhiều năm nhị cạnh góc vuông của tam giác.
_HOOK_
Xem thêm: zalo đã nhận là xem chưa
Nếu biết chiều nhiều năm cạnh lòng và độ cao của tam giác, thực hiện thế nào là nhằm tính diện tích?
Để tính diện tích S tam giác lúc biết chiều nhiều năm cạnh lòng và độ cao của tam giác, tớ dùng công thức: S = (a x h) / 2. Trong số đó, S là diện tích S tam giác, a là chiều nhiều năm cạnh lòng và h là độ cao của tam giác.
Công thức này được vận dụng mang đến tam giác thông thường (không đều và ko vuông). Ta chỉ việc nhân chiều nhiều năm cạnh lòng với độ cao, tiếp sau đó phân tách song sản phẩm nhằm tính được diện tích S tam giác.
Ví dụ: Nếu chiều nhiều năm cạnh lòng là 4 centimet và độ cao là 6 centimet, tớ rất có thể tính diện tích S tam giác theo đòi công thức: S = (4 x 6) / 2 = 12 cm2. Vậy diện tích S tam giác là 12 cm2.
Công thức tính diện tích S tam giác với những công thức không giống nhau không?
Có, công thức tính diện tích S tam giác rất có thể được vận dụng theo đòi vô số cách thức không giống nhau. Công thức thông dụng nhất nhằm tính diện tích S tam giác là S = (a x h)/2, vô bại a là chừng nhiều năm của cạnh lòng tam giác và h là chừng nhiều năm độ cao ứng với cạnh lòng bại. Tuy nhiên, tùy vô vấn đề nhưng mà tất cả chúng ta với, rất có thể vận dụng những công thức không giống nhằm tính diện tích S tam giác, như dùng chừng nhiều năm những cạnh, dùng quyết định lý Pythagoras, hoặc dùng những quy tắc về góc và cạnh của tam giác.
.jpg)
Diện tích tam giác - Toán nâng lên lớp 5 - Thầy Nguyễn Thành Long
Muốn gia tăng kiến thức và kỹ năng Toán nâng lên lớp 5 của mình? Xem Clip này nhằm mò mẫm hiểu về những câu hỏi thú vị và cơ hội xử lý bọn chúng một cơ hội giản dị tuy nhiên hiệu suất cao nhất.
Diện tích tam giác - Toán lớp 5 - Cô Hà Phương
Bạn tiếp tục biết công thức diện tích S tam giác tuy nhiên ko làm rõ về phong thái vận dụng vô thực tế? Đừng bỏ qua Clip này, các bạn sẽ được chỉ dẫn cụ thể và minh họa bằng phương pháp thực tiễn về công thức diện tích S tam giác.
Tại sao tớ cần phân tách tỷ trọng diện tích S tam giác mang đến 2?
Nguyên tắc phân tách diện tích S tam giác mang đến 2 là vì thế công thức tính diện tích S của tam giác được kiến thiết dựa vào nguyên tắc coi tam giác như 1/2 hình chữ nhật. Khi tớ lấy chiều nhiều năm cạnh lòng của tam giác nhân với độ cao của tam giác và phân tách tỷ trọng mang đến 2, tớ đang được tạo nên một hình chữ nhật với diện tích S tương tự với 1/2 diện tích S của tam giác. Do bại, nhằm tính đúng mực diện tích S tam giác, tớ cần phân tách tỷ trọng này mang đến 2.
Có phương pháp tính diện tích S tam giác nào là không giống ko dựa vào độ cao và đáy?
Có, ngoài phương pháp tính diện tích S tam giác vị công thức độ cao nhân lòng phân tách 2, tớ cũng rất có thể dùng công thức Heron hoặc công thức Sarrus nhằm tính diện tích S tam giác.
1. Công thức Heron:
Công thức Heron là 1 công thức được dùng nhằm tính diện tích S tam giác Khi tớ biết chừng nhiều năm tía cạnh của tam giác. Công thức Heron được viết lách như sau: S = √(p(p-a)(p-b)(p-c)), vô bại S là diện tích S tam giác, a, b, c theo thứ tự là chừng nhiều năm tía cạnh của tam giác và p là nửa chu vi của tam giác theo đòi công thức p = (a+b+c)/2.
2. Công thức Sarrus:
Công thức Sarrus là 1 công thức được dùng nhằm tính diện tích S tam giác Khi tớ biết tọa chừng tía đỉnh của tam giác. Công thức Sarrus được viết lách như sau: S = 1/2[(x₁y₂ + x₂y₃ + x₃y₁) - (y₁x₂ + y₂x₃ + y₃x₁)], vô bại (x₁, y₁), (x₂, y₂), (x₃, y₃) theo thứ tự là tọa chừng của tía đỉnh của tam giác.
Tuy nhiên, công thức Heron và công thức Sarrus thông thường được dùng nhằm tính diện tích S tam giác trong số tình huống quan trọng như tam giác ko vuông hoặc Khi tớ biết chừng nhiều năm tía cạnh hoặc tọa chừng tía đỉnh của tam giác. Cách tính diện tích S tam giác vị độ cao nhân lòng phân tách 2 là cách thức thông dụng và giản dị nhất vô lớp 5.
Xem thêm: vẽ về ước mơ của em
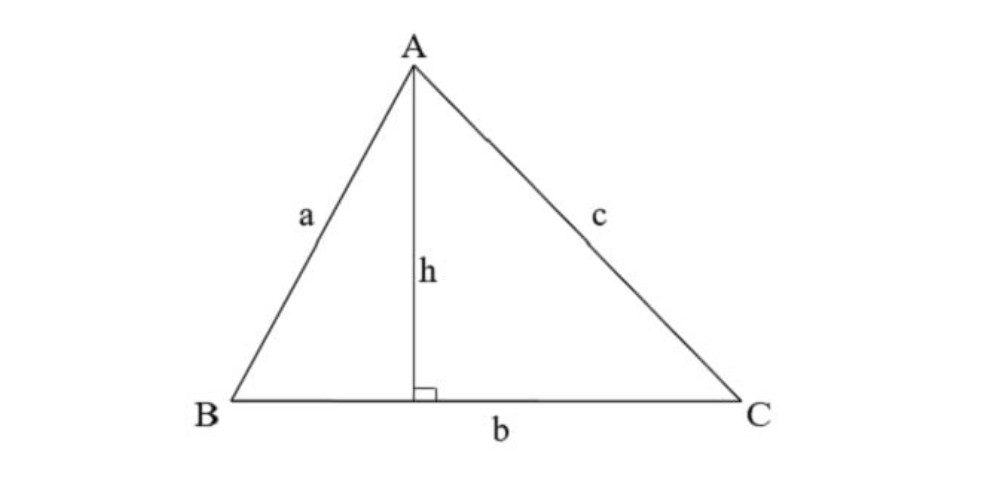
Lớp nào là học tập về công thức tính diện tích S tam giác?
Công thức tính diện tích S tam giác được học tập vô môn Toán, và thường thì được giảng dạy dỗ kể từ lớp 5 trở chuồn. Học sinh kể từ lớp 5 trở chuồn sẽ tiến hành học tập về diện tích S tam giác và những công thức tương quan, như công thức tính diện tích S tam giác thông thường, công thức Hê-ron nhằm tính diện tích S tam giác đều lúc biết chừng nhiều năm những cạnh, và những công thức tính diện tích S tam giác quan trọng không giống.
_HOOK_









Bình luận