Chủ đề đặc điểm lối trung tuyến trong tam giác vuông: Đường trung tuyến trong tam giác vuông với đặc điểm đặc biệt quan trọng và hữu ích. Khi một lối trung tuyến ứng với cạnh huyền của tam giác vuông vì thế một nửa cạnh huyền, tớ hoàn toàn có thể đơn giản đo lường và tính toán những đoạn trực tiếp nhập tam giác. Đây là 1 đặc điểm ấn tượng chung tất cả chúng ta xử lý những câu hỏi tương quan cho tới tam giác vuông một cơ hội nhanh gọn lẹ và đúng mực.
Tính hóa học lối trung tuyến trong tam giác vuông là gì?
Tính hóa học của lối trung tuyến trong tam giác vuông là như sau:
- Đường trung tuyến trong tam giác vuông là đoạn trực tiếp nối kể từ đỉnh của tam giác cho tới trung điểm của cạnh đối lập.
- Mỗi tam giác vuông sẽ sở hữu 3 lối trung tuyến, từng lối trung tuyến chính thức từ là một đỉnh và kết cổ động bên trên trung điểm của cạnh đối lập.
- Trong tam giác vuông, lối trung tuyến ứng với cạnh huyền với Điểm lưu ý đặc biệt quan trọng. Độ nhiều năm của lối trung tuyến này vì thế 50% phỏng nhiều năm của cạnh huyền.
- Nếu biết trọng tâm, lối trung tuyến trong tam giác vuông cũng trải qua trọng tâm của tam giác.
- Đường trung tuyến trong tam giác vuông không chỉ là là 1 phần của tam giác mà còn phải tạo ra trở thành một tam giác không giống cùng theo với đỉnh của tam giác lúc đầu.
- Các lối trung tuyến trong tam giác vuông với tầm quan trọng cần thiết trong các công việc xác lập trọng tâm và tăng cao tính ổn định toan của tam giác.
Bạn đang xem: trung tuyến trong tam giác vuông

Đường trung tuyến trong tam giác vuông với tầm quan trọng gì?
Đường trung tuyến trong tam giác vuông là đoạn trực tiếp nối kể từ đỉnh vuông góc của tam giác cho tới trung điểm của cạnh đối lập đỉnh vuông góc cơ. Đường trung tuyến trong tam giác vuông với tầm quan trọng cần thiết trong các công việc dò la những đặc điểm và đặc điểm của tam giác vuông. Dưới đó là những tầm quan trọng chủ yếu của lối trung tuyến trong tam giác vuông:
1. Đường trung tuyến phân tách hai đường tròn trĩnh nước ngoài tiếp tam giác: Đường trung tuyến trong tam giác vuông phân tách hai đường tròn trĩnh nước ngoài tiếp tam giác. Như vậy tức là phỏng nhiều năm đoạn phân tách song bên trên lối tròn trĩnh nước ngoài tiếp vì thế 50% 2 lần bán kính của lối tròn trĩnh nước ngoài tiếp. Như vậy thông thường cực kỳ hữu ích trong các công việc đo lường và tính toán những độ quý hiếm tương quan cho tới tam giác vuông.
2. Đường trung tuyến với đặc điểm gấp hai lối bình phương: Đường trung tuyến trong tam giác vuông với đặc điểm nhất là lối trung tuyến có tính nhiều năm vì thế gấp hai bình phương của nửa lối chéo cánh. Như vậy hoàn toàn có thể được dùng nhằm đo lường và tính toán những tỷ trọng trong số những cạnh và lối trung tuyến trong tam giác vuông.
3. Đường trung tuyến là lối cao nhập tam giác đồng dạng: Trong tam giác vuông, lối trung tuyến cũng chính là lối cao của tam giác vuông đồng dạng. Như vậy tức là đoạn kể từ đỉnh vuông góc cho tới trung điểm của cạnh đối lập vuông góc là lối cao của tam giác vuông đồng dạng với tam giác lúc đầu. Như vậy hoàn toàn có thể được dùng nhằm đo lường và tính toán những tỷ trọng và mối liên hệ trong số những thành phần nhập tam giác đồng dạng.
Tóm lại, lối trung tuyến trong tam giác vuông với tầm quan trọng cần thiết trong các công việc dò la tìm tòi những đặc điểm và đo lường và tính toán những độ quý hiếm tương quan cho tới tam giác vuông. Việc hiểu và dùng những đặc điểm của lối trung tuyến sẽ hỗ trợ tất cả chúng ta xử lý những câu hỏi tương quan cho tới tam giác vuông một cơ hội hiệu suất cao.
Tam giác vuông với từng nào lối trung tuyến?
Một tam giác vuông với tía lối trung tuyến. Đường trung tuyến nhập tam giác là 1 đoạn trực tiếp nối kể từ đỉnh của tam giác cho tới trung điểm của cạnh đối lập. Mỗi tam giác vuông sẽ sở hữu một lối trung tuyến ứng với từng cạnh của tam giác. Vì vậy, tam giác vuông với tía cạnh, vì thế với tía lối trung tuyến.
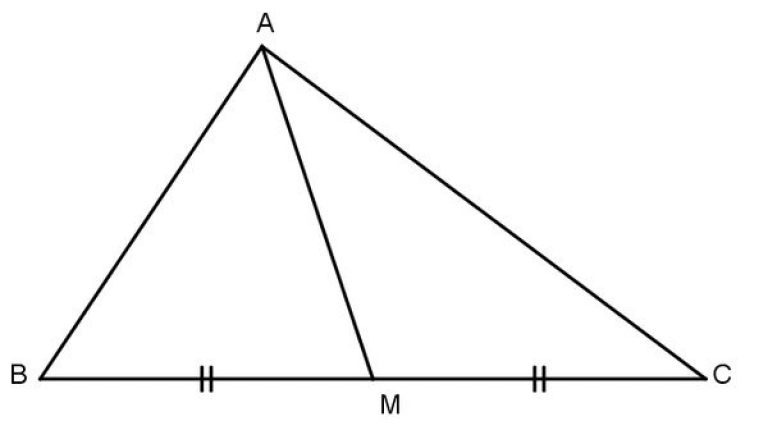
Trung tuyến tam giác vuông với cạnh huyền vì thế nửa cạnh huyền
Tam giác vuông là 1 trong mỗi hình học tập đặc biệt quan trọng hấp dẫn sự xem xét của người tiêu dùng. quý khách vẫn muốn dò la hiểu về những đặc điểm vi diệu của tam giác vuông? Hãy coi đoạn phim này nhằm tìm hiểu nhiều điều thú vị về tam giác vuông và phần mềm của chính nó nhập thực tiễn.
Tính hóa học tía lối trung tuyến tam giác - Bài 4 - Toán học tập 7 - Cô Nguyễn Thu Hà
Đường trung tuyến nhập tam giác là 1 định nghĩa thú vị. Hãy coi đoạn phim nhằm làm rõ về tầm quan trọng của lối trung tuyến và những đặc điểm đặc biệt quan trọng của chính nó. quý khách tiếp tục kinh ngạc lúc biết được phần mềm thực tiễn của lối trung tuyến nhập cuộc sống đời thường mỗi ngày.
Làm sao nhằm tính phỏng nhiều năm lối trung tuyến trong tam giác vuông?
Để tính phỏng nhiều năm lối trung tuyến trong tam giác vuông, tất cả chúng ta hoàn toàn có thể thực hiện như sau:
Bước 1: Xác toan tam giác vuông với những cạnh a, b và c. Trong tam giác vuông, cạnh huyền luôn luôn là cạnh lớn số 1 và được ký hiệu là c.
Bước 2: Tìm trung điểm của cạnh huyền. Trung điểm của một quãng trực tiếp là vấn đề nằm ở vị trí thân ái đoạn trực tiếp cơ. Vì cạnh huyền của tam giác vuông phân tách tam giác thực hiện nhị tam giác nhỏ nằm trong hình dạng, nên điểm trung điểm của cạnh huyền cũng đó là trung điểm của cạnh đối lập với cạnh huyền. Gọi đỉnh của tam giác vuông là A, trung điểm của cạnh huyền là M.
Bước 3: Tính phỏng nhiều năm lối trung tuyến. Đường trung tuyến trong tam giác vuông là đoạn trực tiếp nối kể từ đỉnh của tam giác cho tới trung điểm của cạnh đối lập. Vì tam giác vuông với đỉnh A và trung điểm M, nên đoạn trực tiếp AM đó là lối trung tuyến cần thiết tính phỏng nhiều năm.
Trong tam giác vuông, lối trung tuyến với vì thế từng nào cạnh rất khác góc vuông?
Trong tam giác vuông, lối trung tuyến rất khác góc vuông có tính nhiều năm vì thế 50% phỏng nhiều năm cạnh rất khác góc vuông cơ. Để tính được phỏng nhiều năm lối trung tuyến, tớ hoàn toàn có thể tuân theo quá trình sau:
1. Xác toan cạnh rất khác góc vuông của tam giác vuông.
2. Tính phỏng nhiều năm cạnh rất khác góc vuông bằng phương pháp dùng công thức Pythagoras: a² = b² + c², với a là cạnh rất khác góc vuông, b là cạnh góc vuông và c là cạnh sót lại.
3. Chia phỏng nhiều năm cạnh rất khác góc vuông cho tới 2 nhằm tính phỏng nhiều năm lối trung tuyến.
Ví dụ, fake sử cạnh rất khác góc vuông của tam giác vuông ABC có tính nhiều năm là 10 đơn vị chức năng. Ta hoàn toàn có thể tính phỏng nhiều năm lối trung tuyến như sau:
1. Cạnh rất khác góc vuông của tam giác ABC là cạnh AB.
2. Sử dụng công thức Pythagoras: AB² = BC² + AC².
3. bằng phẳng cơ hội thay cho độ quý hiếm những cạnh nhập công thức, tớ có: AB² = 10² + AC² ==> 100 = 100 + AC² ==> AC² = 0. Do cơ, cạnh sót lại có tính nhiều năm vì thế 0, tức là tam giác là tam giác thông thường, ko cần tam giác vuông.
Vậy, nhập tam giác vuông, lối trung tuyến có tính nhiều năm vì thế 50% cạnh rất khác góc vuông.

_HOOK_
Đường trung tuyến trong tam giác vuông với nằm trong phỏng nhiều năm rất khác lối cao?
Để vấn đáp thắc mắc này, tớ cần thiết làm rõ về đặc điểm của lối trung tuyến và lối cao nhập tam giác vuông.
1. Đường trung tuyến (AM) nhập tam giác vuông là đường thẳng liền mạch nối kể từ đỉnh vuông của tam giác cho tới trung điểm của cạnh đối lập (BC).
2. Đường cao (AH) nhập tam giác vuông cũng chính là đường thẳng liền mạch nối kể từ đỉnh vuông cho tới đỉnh của cạnh huyền (AB hoặc AC), vuông góc với cạnh huyền.
Giờ tớ tiếp tục minh chứng rằng lối trung tuyến (AM) và lối cao (AH) nhập tam giác vuông không tồn tại nằm trong phỏng nhiều năm.
Giả sử tớ với tam giác vuông ABC, với cạnh huyền là AB và AM là lối trung tuyến.
Theo đặc điểm của cạnh huyền nhập tam giác vuông, tớ hiểu được cạnh huyền vì thế gấp hai cạnh góc vuông. Ta với AB = 2AC.
Giả sử AH là lối cao, tức thị AH vuông góc với AB và AH là lối trải qua đỉnh vuông (A).
Ta hiểu được lối cao AH phân tách cạnh huyền AB trở thành 2 đoạn tương tự. Một đoạn là x và đoạn sót lại là 2x, với x là chiều nhiều năm của đoạn kể từ đỉnh vuông cho tới điểm phân tách.
Theo toan lý Pythagoras, tớ có: AB² = AC² + BC².
Với tam giác vuông ABC, tớ với AB = 2AC, nên tớ với (2AC)² = AC² + BC².
Rút gọn gàng phương trình, tớ được: 4AC² = AC² + BC².
Tiếp tục rút gọn gàng, tớ với 3AC² = BC².
Từ trên đây, tớ rút đi ra được AC = BC/√3.
Theo đặc điểm của tam giác đều, tớ hiểu được trung tuyến AM phân tách cạnh huyền AB trở thành 2 đoạn tương tự. Một đoạn là nó và đoạn sót lại là 2y, với nó là chiều nhiều năm của đoạn kể từ đỉnh vuông cho tới điểm phân tách.
Ta hiểu được AM = AC + CM.
Ta vẫn với AC = BC/√3, và vì thế CM là nửa cạnh BC, nên tớ với CM = BC/2.
Thay nhập công thức bên trên, tớ với AM = BC/√3 + BC/2.
Rút gọn gàng phân số, tớ được AM = (2BC + 3BC√3)/(2√3).
Từ trên đây, tớ hoàn toàn có thể thấy rằng AM ko vì thế AH, vì thế AM và AH với công thức đo lường và tính toán không giống nhau.
Vì vậy, lối trung tuyến và lối cao nhập tam giác vuông không tồn tại nằm trong phỏng nhiều năm.
Điểm bên trên lối trung tuyến phân tách hai đường trung tuyến là vấn đề gì?
Điểm bên trên lối trung tuyến phân tách hai đường trung tuyến là trung điểm của đoạn trực tiếp cơ. Trên từng lối trung tuyến không chỉ là với 1 điểm phân tách song, nhưng mà toàn bộ đều phân tách song ở và một điểm, cơ đó là trung điểm của đoạn trực tiếp cơ. Vì vậy, điểm bên trên lối trung tuyến phân tách hai đường trung tuyến là trung điểm.
Trung điểm của đoạn trực tiếp nối thân ái đỉnh và góc vuông của tam giác vuông được gọi là gì?
Trung điểm của đoạn trực tiếp nối thân ái đỉnh và góc vuông của tam giác vuông được gọi là lối trung tuyến trong tam giác vuông. Đường trung tuyến là 1 đoạn trực tiếp nối kể từ đỉnh của tam giác cho tới trung điểm của cạnh đối lập. Trong tam giác vuông, với tía lối trung tuyến ứng với tía cạnh của tam giác.
Xem thêm: góc nhọn bao nhiêu độ
Phân biệt lối trung tuyến, lối trung trực, lối cao, lối phân giác tam giác
Đường trung trực là 1 định nghĩa cần thiết nhập hình học tập. Hãy nằm trong coi đoạn phim nhằm dò la hiểu về lối trung trực và những đặc điểm xứng đáng quá bất ngờ của chính nó. quý khách tiếp tục nhìn thấy sự tác động của lối trung trực nhập hình học tập và phần mềm thực tiễn của chính nó.
Tính hóa học 3 lối trung tuyến tam giác - Toán 7
Đường cao là 1 định nghĩa mê hoặc nhập tam giác. Nếu mình muốn làm rõ về đặc điểm đặc biệt quan trọng của lối cao và phần mềm của chính nó, hãy coi đoạn phim này. quý khách tiếp tục tìm hiểu những điều thú vị về lối cao và sự tương quan của chính nó cho tới tam giác.
Tính hóa học của lối trung tuyến ứng với cạnh góc vuông nhập tam giác vuông?
Đường trung tuyến ứng với cạnh góc vuông nhập tam giác vuông với những đặc điểm sau:
1. Đường trung tuyến là đoạn trực tiếp nối đỉnh của tam giác với trung điểm của cạnh góc vuông.
2. Đường trung tuyến có tính nhiều năm vì thế 50% phỏng nhiều năm cạnh góc vuông.
3. Đường trung tuyến là lối cao và lối khoảng của tam giác vuông.
4. Đường trung tuyến phân tách song diện tích S của tam giác vuông.
5. Đường trung tuyến vuông góc với cạnh góc vuông và tách cạnh góc vuông trở thành nhị phần cân nhau.
6. Đường trung tuyến là lối trục đối xứng của tam giác vuông, tạo ra trở thành hình đối xứng qua loa lối trung tuyến.
Những đặc điểm này hoàn toàn có thể được vận dụng và minh chứng trong số câu hỏi tương quan cho tới tam giác vuông và lối trung tuyến.
Đường trung tuyến trong tam giác vuông với cộng đồng điểm với lối cao không?
Trong tam giác vuông, lối trung tuyến ko cộng đồng điểm với lối cao. Để minh chứng điều này, tất cả chúng ta hoàn toàn có thể dùng những đặc điểm của tam giác vuông.
Đường trung tuyến là đoạn trực tiếp nối kể từ đỉnh của tam giác cho tới trung điểm của cạnh đối lập. Trong tam giác vuông, cạnh huyền là cạnh đối lập với góc vuông. Do cơ, lối trung tuyến ứng với cạnh huyền đó là lối cao của tam giác.
Vì vậy, lối trung tuyến trong tam giác vuông chỉ cộng đồng điểm với 1 lối cao độc nhất, này đó là lối trọng tâm. Đường này trải qua trọng tâm của tam giác. Đường cao sót lại, tức là lối cao ko cộng đồng điểm với lối trung tuyến.
_HOOK_
Trong tam giác vuông, lối trung tuyến liệu có phải là lối phân giác của góc không?
Trong tam giác vuông, lối trung tuyến ko cần là lối phân giác của góc. Đường trung tuyến trong tam giác vuông là đoạn trực tiếp nối kể từ đỉnh của tam giác cho tới trung điểm của cạnh đối lập. Như vậy tức là lối trung tuyến phân tách cạnh đối lập trở thành nhị phần cân nhau.
Đường phân giác của góc nhập tam giác là đường thẳng liền mạch phân tách góc cơ trở thành nhị góc nhỏ cân nhau. Trong tam giác vuông, lối phân giác của góc vuông được xem là đường thẳng liền mạch trải qua đỉnh của góc vuông và trung điểm của cạnh đối lập góc cơ.
Do cơ, nhập tam giác vuông, lối trung tuyến ko trùng với lối phân giác của góc vuông.
Tính hóa học của lối trung tuyến ứng với cạnh đối lập góc vuông nhập tam giác vuông?
Tính hóa học của lối trung tuyến ứng với cạnh đối lập góc vuông nhập tam giác vuông là phỏng nhiều năm lối trung tuyến vì thế 50% phỏng nhiều năm cạnh đối lập góc vuông.
Cụ thể, nhập tam giác vuông ABC với góc vuông ở đỉnh A và cạnh BC là cạnh đối lập góc vuông, tớ có:
- Đường trung tuyến nằm trong phía với cạnh BC là lối nối kể từ đỉnh A cho tới trung điểm M của cạnh BC.
- Tính hóa học lối trung tuyến: Độ nhiều năm lối trung tuyến AM vì thế 50% phỏng nhiều năm cạnh BC, tức là AM = một nửa BC.
Như vậy, tớ hoàn toàn có thể suy đi ra rằng lối trung tuyến ứng với cạnh đối lập góc vuông nhập tam giác vuông luôn luôn có tính nhiều năm vì thế 50% phỏng nhiều năm cạnh đối lập góc vuông.
Trong tam giác vuông, lối trung tuyến và lối cao với phú điểm không?
Trong tam giác vuông, lối trung tuyến và lối cao tiếp tục luôn luôn với phú điểm. Để minh chứng điều này, tớ hoàn toàn có thể dùng một trong những đặc điểm của tam giác vuông và tam giác đồng dạng.
Giả sử nhập tam giác vuông ABC, lối cao kể từ đỉnh A tách cạnh BC bên trên điểm H, và lối trung tuyến kể từ đỉnh A tách cạnh BC bên trên điểm M. Ta cần thiết minh chứng rằng điểm M phía trên lối cao AH.
Bước 1: Ta hiểu được lối cao AH phân tách cạnh BC trở thành nhị đoạn bám theo tỷ trọng vì thế phỏng nhiều năm những cạnh AB và AC. Nghĩa là:
\\(\\dfrac{BH}{CH} = \\dfrac{AB^2}{AC^2}\\) (1)
Bước 2: Ta hiểu được lối trung tuyến vẫn phân tách cạnh BC trở thành nhị đoạn với tỷ trọng vì thế 1:1. Nghĩa là:
\\(\\dfrac{BM}{MC} = 1\\) (2)
Bước 3: Ta cần thiết minh chứng rằng điểm M phía trên lối cao AH, tức là:
\\(\\dfrac{BH}{CH} = \\dfrac{BM}{MC}\\) (3)
Bước 4: Kết phù hợp những biểu thức (1) và (2), tớ có:
\\(\\dfrac{AB^2}{AC^2} = \\dfrac{BM}{MC}\\)
Do cơ, biểu thức (3) được minh chứng trúng.
Vậy, tớ Tóm lại rằng lối trung tuyến và lối cao nhập tam giác vuông với phú điểm.
Toán 7 - Bài 4 - Tính hóa học tía lối trung tuyến tam giác - Tiết 1
Đường phân giác là 1 trong mỗi định nghĩa cần thiết nhập hình học tập. Hãy coi đoạn phim này nhằm làm rõ về đặc điểm đặc biệt quan trọng của lối phân giác và cơ hội nó được dùng nhập thực tiễn. quý khách tiếp tục tìm hiểu những phần mềm thú vị của lối phân giác nhập cuộc sống đời thường mỗi ngày.
Tam giác vuông hoàn toàn có thể với lối trung tuyến cân nhau không?
Trong tam giác vuông, lối trung tuyến là đoạn trực tiếp nối kể từ đỉnh của tam giác cho tới trung điểm của cạnh đối lập. Mỗi tam giác vuông sẽ sở hữu 3 lối trung tuyến, tạo ra trở thành tía đoạn trực tiếp nối trung điểm của những cạnh với đỉnh ứng.
Khi xét về đặc điểm lối trung tuyến trong tam giác vuông:
1. Đường trung tuyến ứng với cạnh huyền của tam giác vuông tiếp tục vì thế 50% cạnh huyền cơ. Như vậy hoàn toàn có thể được minh chứng bằng phương pháp dùng toan lý Pythagoras và tính tỉ trọng phỏng nhiều năm cạnh của tam giác vuông.
2. Đường trung tuyến ứng với 1 cạnh không giống ko cần cạnh huyền sẽ sở hữu phỏng nhiều năm nhỏ rộng lớn lối trung tuyến ứng với cạnh huyền. Như vậy cũng hoàn toàn có thể được minh chứng bằng phương pháp dùng toan lý Pythagoras và tính tỉ trọng phỏng nhiều năm cạnh của tam giác vuông.
Vì vậy, từng tam giác vuông với những lối trung tuyến có tính nhiều năm không giống nhau, ko cân nhau.
Đường trung tuyến trong tam giác vuông với tầm quan trọng cần thiết trong số câu hỏi hình học tập nào?
Đường trung tuyến trong tam giác vuông với tầm quan trọng cần thiết trong số câu hỏi hình học tập sau:
1. Tính phỏng nhiều năm lối trung tuyến: Đối với tam giác vuông, tớ hiểu được lối trung tuyến ứng với cạnh huyền có tính nhiều năm vì thế 50% cạnh huyền. Ví dụ, nếu như cạnh huyền là 10 đơn vị chức năng, thì lối trung tuyến ứng với cạnh huyền sẽ sở hữu phỏng nhiều năm là 5 đơn vị chức năng.
2. Đứng vuông góc: Đường trung tuyến tách nhau vuông góc bên trên trung điểm của cạnh đối lập. Như vậy hoàn toàn có thể được dùng nhằm minh chứng rằng lối trung tuyến là lối cao, lối khoảng và lối phân giác của tam giác vuông.
3. Tính diện tích S tam giác: Đường trung tuyến phân tách tam giác trở thành nhị tam giác nằm trong diện tích S, những tam giác này còn có đỉnh chung trung điểm và cạnh cộng đồng là lối trung tuyến. Do cơ, Lúc tính diện tích S của tam giác vuông, tớ hoàn toàn có thể dùng diện tích S của một trong những nhị tam giác nhỏ rộng lớn.
4. Xác toan trung điểm: Đường trung tuyến cũng chung xác lập trung điểm của một cạnh. Ví dụ, nhập tam giác vuông, lối trung tuyến kể từ đỉnh chỉ qua loa trung điểm của cạnh đối lập tiếp tục trải qua trung điểm của cạnh cơ.
5. Chứng minh đẳng thức: Đường trung tuyến cũng hoàn toàn có thể được dùng nhằm minh chứng đẳng thức trong số câu hỏi tam giác. Ví dụ, lối trung tuyến của tam giác vuông phân tách tam giác trở thành nhị phần với diện tích S cân nhau, điều này hoàn toàn có thể được dùng nhằm minh chứng những đẳng thức tương quan cho tới diện tích S tam giác.
Đường trung tuyến trong tam giác vuông là 1 dụng cụ hữu ích nhằm xử lý nhiều câu hỏi hình học tập tương quan cho tới tam giác vuông.
Xem thêm: say đắm trong lần đầu
_HOOK_
Chứng minh tiếp tuyến phố tròn trĩnh và lối trung tuyến trong tam giác vuông
- Video này tiếp tục hỗ trợ cho chính mình những minh chứng logic và chan chứa thuyết phục về những đặc điểm nhập toán học tập. - quý khách tiếp tục tiếp cận với cách thức tiếp tuyến chan chứa thú vị và phần mềm của chính nó nhập hàng loạt những câu hỏi tương quan cho tới hình học tập. - Khám phá huỷ những bài xích giảng cụ thể về những đặc điểm của lối tròn trĩnh và cơ hội vận dụng bọn chúng trong số câu hỏi thực tiễn qua loa đoạn phim này. - Hãy dò la hiểu về đặc điểm đặc biệt quan trọng của lối trung tuyến nhập tam giác, và cơ hội bọn chúng giúp chúng ta xử lý những câu hỏi phức tạp. - Điểm qua loa những đặc điểm đặc biệt quan trọng của tam giác vuông và cơ hội bọn chúng hoàn toàn có thể được dùng nhằm xử lý những câu hỏi phức tạp nhập đoạn phim này. - Video này reviews Điểm lưu ý và đặc điểm cơ bạn dạng của những hình học tập, khiến cho bạn hiểu thâm thúy rộng lớn về những hình dạng và quy luật ứng của bọn chúng.












Bình luận