Chủ đề diện tích S hình trụ lúc biết cung cấp kính: Diện tích hình trụ là 1 định nghĩa cần thiết vô toán học tập và hình học tập. Khi biết nửa đường kính của hình trụ, tất cả chúng ta rất có thể tính được diện tích S của chính nó. Công thức đơn giản và giản dị nhằm tính diện tích hình tròn là nhân nửa đường kính với bình phương của số Pi. Vấn đề này gom tất cả chúng ta nắm rõ rộng lớn và đơn giản dễ dàng đo lường diện tích S những hình trụ vô cuộc sống đời thường mỗi ngày.
Tính diện tích S hình trụ lúc biết cung cấp kính
Để tính diện tích hình tròn Lúc chỉ biết nửa đường kính, tao dùng công thức sau:
Diện tích (S) = π * (bán kính)^2
Trong cơ, π (pi) là 1 hằng số xấp xỉ vì chưng 3.14, nửa đường kính là chừng lâu năm kể từ trung điểm đến lựa chọn ngẫu nhiên điểm nào là bên trên lối viền hình trụ.
Ví dụ: Giả sử nửa đường kính của hình trụ là R, nhằm tính diện tích S (S), tao tiến hành công việc sau đây:
1. Gán độ quý hiếm lúc đầu mang lại nửa đường kính R.
2. Tính diện tích S trải qua công thức: S = 3.14 * R^2. Đối với những độ quý hiếm nửa đường kính không giống nhau, thay cho thế R vì chưng độ quý hiếm ứng và đo lường.
3. Sau Lúc đo lường, tao với diện tích S của hình trụ.
Ví dụ: Nếu nửa đường kính hình trụ là 5 centimet, tao tính diện tích S như sau:
S = 3.14 * 5^2 = 3.14 * 25 = 78.5 (cm^2)
Vậy diện tích S của hình trụ với nửa đường kính là 5 centimet là 78.5 cm^2.
Bạn đang xem: tính diện tích hình tròn
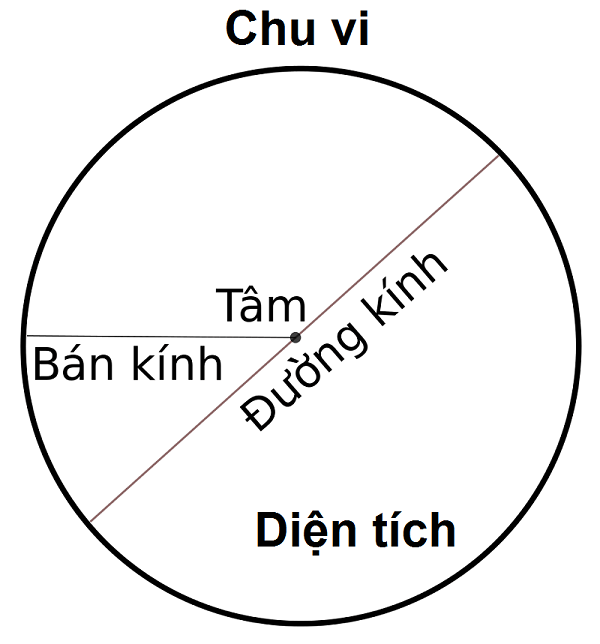
Diện tích của hình trụ được xem ra sao lúc biết cung cấp kính?
Để tính diện tích S của hình trụ lúc biết nửa đường kính, tao vận dụng công thức sau: Diện tích = pi x cung cấp kính^2.
Bước 1: Xác định vị trị của nửa đường kính (R) của hình trụ.
Bước 2: Tiến hành đo lường diện tích S bằng phương pháp thay cho vô công thức: Diện tích = 3.14 x R^2.
Ví dụ: Giả sử nửa đường kính của hình trụ là 5cm.
Diện tích = 3.14 x 5^2 = 3.14 x 25 = 78.5 cm^2.
Vậy diện tích S của hình trụ với nửa đường kính là 5cm là 78.5 cm^2.
Bán kính là gì và làm thế nào nhằm tính nửa đường kính của một hình tròn?
Bán kính của một hình trụ là khoảng cách kể từ tâm của hình trụ cho tới ngẫu nhiên điểm nào là bên trên lối viền của chính nó. Để tính nửa đường kính của một hình trụ, chúng ta có thể tuân theo công việc sau:
Bước 1: Tìm tâm của hình trụ. Tâm của một hình trụ được xác lập bằng phương pháp lấy trung điểm của những đoạn trực tiếp nối nhì điểm bên trên lối viền của hình trụ.
Bước 2: Chọn ngẫu nhiên điểm nào là bên trên lối viền của hình trụ. Đo chừng lâu năm kể từ tâm của hình trụ tới điểm cơ. Kết trái ngược này đó là nửa đường kính của hình trụ.
Ví dụ, fake sử chúng ta với cùng 1 hình trụ và ham muốn tính nửa đường kính của chính nó. Quý Khách rất có thể thực hiện như sau:
Bước 1: Tìm tâm của hình trụ. Vẽ hai tuyến đường trung trực vuông góc cùng nhau bên trên nhì đoạn trực tiếp rời nhau bên trên điểm O. Điểm O đó là tâm của hình trụ.
Bước 2: Chọn một điểm ngẫu nhiên bên trên lối viền của hình trụ, ví dụ điểm A.
Bước 3: Sử dụng thước đo đo chừng lâu năm kể từ tâm của hình trụ (điểm O) cho tới điểm A. Kết trái ngược này đó là nửa đường kính của hình trụ.
Lưu ý rằng nửa đường kính của một hình trụ tiếp tục tương đương nhau mang lại toàn bộ những điểm bên trên lối viền của chính nó.

Công thức tính diện tích hình tròn lúc biết nửa đường kính là gì?
Công thức tính diện tích hình tròn lúc biết nửa đường kính là: Diện tích = pi * nửa đường kính * nửa đường kính, hoặc bên dưới dạng không giống là Diện tích = 3.14 * nửa đường kính * nửa đường kính. Đơn vị của diện tích S tiếp tục tùy theo đơn vị chức năng của nửa đường kính (ví dụ: cm², m²).
Làm thế nào là nhằm gửi kể từ nửa đường kính trở thành 2 lần bán kính vô hình tròn?
Để gửi kể từ nửa đường kính trở thành 2 lần bán kính vô hình trụ, tao với công thức sau:
Đường kính (D) = 2 * nửa đường kính (R)
Với nửa đường kính (R) là chừng lâu năm kể từ tâm của hình trụ cho tới ngẫu nhiên điểm nào là bên trên vòng tròn trĩnh.
Ví dụ: Nếu nửa đường kính (R) của hình trụ là 5 centimet, tao rất có thể tính được 2 lần bán kính như sau:
Đường kính (D) = 2 * 5 cm
= 10 cm
Vậy, Lúc nửa đường kính của hình trụ tiếp tục biết, tao rất có thể tính được 2 lần bán kính bằng phương pháp nhân nửa đường kính cơ với 2.

_HOOK_
Cách tính diện tích hình tròn siêu hay
Tìm hiểu cơ hội tính diện tích hình tròn tức thì bên trên Clip này! Với những công thức đơn giản và giản dị và lý giải cụ thể, các bạn sẽ nhanh gọn lẹ thâu tóm được phương pháp tính diện tích S của hình trụ một cơ hội đơn giản dễ dàng và hiệu suất cao.
Xem thêm: cuối tuần này thì sao
Công thức hình tròn: Tìm Vi, Diện Tích, Đường Kính, Bán Kính, Suy Luận Tìm Bán Kính Hình Tròn
Bạn ham muốn lần hiểu công thức hình trụ một cơ hội đơn giản và giản dị và dễ dàng hiểu? Hãy coi Clip này! Chúng tôi tiếp tục hỗ trợ cho chính mình những công thức căn phiên bản và cơ hội vận dụng bọn chúng nhằm đo lường những thông số kỹ thuật cần thiết của hình trụ.
Có thể tính được diện tích S hình trụ chỉ dựa vào 2 lần bán kính không?
Có thể tính được diện tích S hình trụ chỉ dựa vào 2 lần bán kính. Khi biết 2 lần bán kính d, tao rất có thể tính nửa đường kính R bằng phương pháp phân tách 2 lần bán kính mang lại nhì, tức là R = d/2. Sau cơ, tao dùng công thức tính diện tích hình tròn: diện tích S = pi * R^2, vô cơ pi là số pi (khoảng 3,14). Chúng tao nhân nửa đường kính R với chủ yếu nó và tiếp sau đó nhân với pi nhằm tính diện tích S.
Diện tích hình trụ với tùy theo đơn vị chức năng của nửa đường kính không?
Diện tích hình trụ ko tùy theo đơn vị chức năng của nửa đường kính. Đặc điểm cộng đồng của diện tích S hình trụ là tỉ trọng thuận với bình phương của nửa đường kính. Công thức tính diện tích hình tròn là S = π * r^2, vô cơ S là diện tích S, π là số Pi (khoảng 3.14), và r là nửa đường kính.
Ví dụ, nếu như nửa đường kính được đo vì chưng mét, diện tích S sẽ tiến hành tính theo đòi mét vuông. Nếu nửa đường kính được đo vì chưng centimet, diện tích S sẽ tiến hành tính theo đòi centimet vuông. Tuy nhiên, đơn vị chức năng của nửa đường kính ko tác động cho tới độ quý hiếm của diện tích S, tuy nhiên là chỉ đơn vị chức năng được dùng nhằm đo và đối chiếu những độ cao thấp.
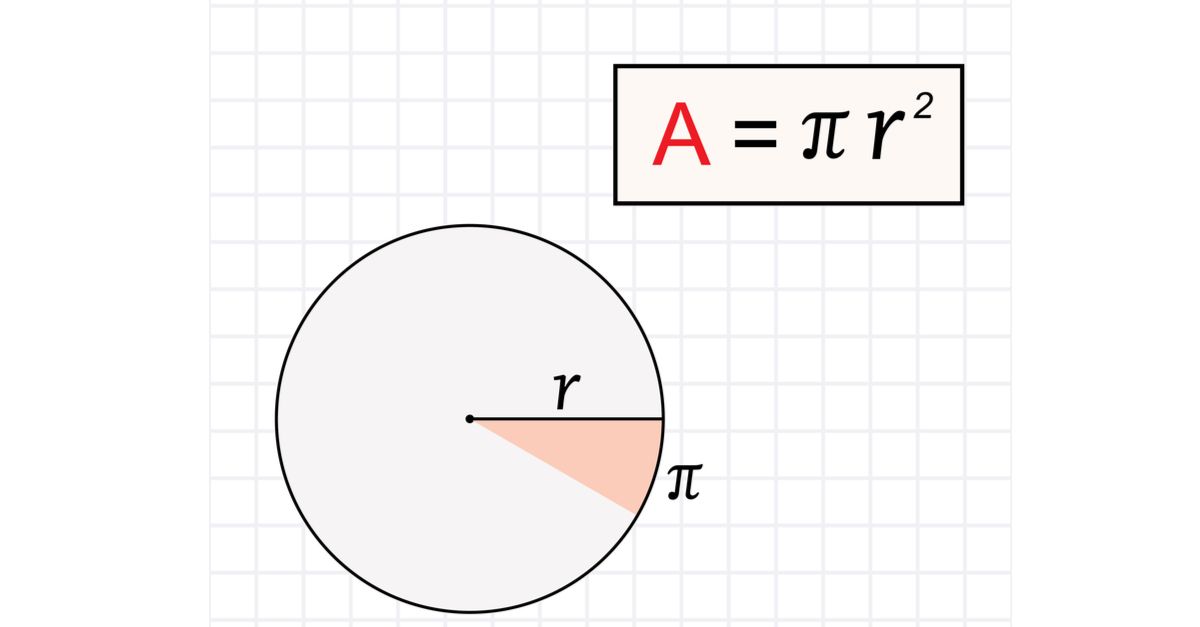
Có những tình huống quan trọng nào là Lúc tính diện tích hình tròn theo đòi cung cấp kính?
Có một số trong những tình huống quan trọng Lúc tính diện tích hình tròn theo đòi nửa đường kính. Dưới đấy là một số trong những tình huống đó:
1. Khi nửa đường kính vì chưng 0: Nếu nửa đường kính của hình trụ là 0, diện tích S của chính nó được xem là 0. Đây là tình huống quan trọng vì thế thành phần hình trụ không tồn tại độ cao thấp nhằm tạo ra diện tích S.
2. Khi nửa đường kính là số âm: Trong toán học tập, nửa đường kính của một hình trụ ko thể là số âm. Do cơ, Lúc tính diện tích hình tròn, tất cả chúng ta ko đánh giá những tình huống này.
3. Khi nửa đường kính là số phức: Vì hình trụ là 1 hình học tập 2 chiều, nửa đường kính cũng cần là một số trong những thực. Số phức ko thể thay mặt đại diện mang lại độ cao thấp so với một hình trụ.
Tuy nhiên, trong những tình huống phổ cập không giống, tao rất có thể tính diện tích hình tròn vì chưng công thức:
Diện tích = π x (bán kính)^2
Trong cơ, π (pi) là 1 hằng số xấp xỉ vì chưng 3.14 với độ quý hiếm đúng chuẩn rộng lớn là 3.14159. Bán kính của hình trụ là chừng lâu năm kể từ trung tâm cho tới ngẫu nhiên điểm nào là bên trên lối viền của chính nó.
Mong rằng vấn đề này giúp cho bạn hiểu về những tình huống quan trọng Lúc tính diện tích hình tròn theo đòi nửa đường kính.
Có cách thức nào là không giống nhằm tính diện tích hình tròn ko trải qua cung cấp kính?
Có, ngoài phương pháp tính trải qua nửa đường kính, tao cũng rất có thể tính diện tích hình tròn trải qua 2 lần bán kính của chính nó. Phương pháp này cũng khá đơn giản và giản dị và dễ nắm bắt. Để tính diện tích hình tròn trải qua 2 lần bán kính, tao người sử dụng công thức sau:
Diện tích (S) = π * (đường kính/2)^2
Trong cơ, π là số pi và 2 lần bán kính là chừng lâu năm đo từ là 1 điểm bên trên lối tròn trĩnh qua quýt tâm tới điểm đối lập bên trên lối tròn trĩnh.
Ví dụ, nếu như tao với cùng 1 hình trụ với 2 lần bán kính là 10 centimet, tao rất có thể tính diện tích S như sau:
S = π * (10/2)^2 = π * 5^2 = 25π (cm^2)
Vậy, diện tích S của hình trụ này là 25π cm^2.
![]()
Tại sao diện tích S hình trụ lại được xem vì chưng pi nhân nửa đường kính chuyến hai?
Diện tích của hình trụ được xem vì chưng công thức S = πr^2, vô cơ S là diện tích S hình trụ, π là 1 hằng số xấp xỉ vì chưng 3,14 và r là nửa đường kính của hình trụ.
Công thức này còn có một giải thích đơn giản và giản dị dựa vào để ý hình học tập. Khi phân tách hình trụ trở thành nhiều phần nhỏ tựa như những hình khối nhỏ, tao rất có thể thấy rằng những hình khối này Lúc được xếp ông xã lên nhau tạo ra trở thành một hình trụ to ra thêm. Vấn đề này đã cho thấy diện tích S của hình trụ đích vì chưng tổng diện tích S của những hình khối nhỏ này.
Khi tao phân tách hình trụ trở thành nhiều vòng tròn trĩnh nhỏ với nửa đường kính đều nhau, tao thấy rằng diện tích S của từng vòng tròn trĩnh nhỏ là vì chưng πr^2, với r là nửa đường kính của hình trụ. Vì những vòng tròn trĩnh nhỏ được xếp ông xã lên nhau, nên diện tích S của hình trụ rộng lớn đó là tổng diện tích S của những vòng tròn trĩnh nhỏ.
Với hình trụ với nửa đường kính R, tao rất có thể phân tách nó trở thành nhiều vòng tròn trĩnh nhỏ với nửa đường kính r đều nhau. Khi cơ con số những vòng tròn trĩnh nhỏ vì chưng R/r. Vì vậy diện tích S của hình trụ rộng lớn cũng đó là tổng diện tích S của những vòng tròn trĩnh nhỏ, được xem vì chưng πr^2 nhân con số những vòng tròn trĩnh nhỏ, tức là S = πr^2 x R/r = πRr.
Tuy nhiên, với đặc thù đối xứng của hình trụ, tao rất có thể phân tách nó trở thành nhiều phần nhỏ tương tự động như bên trên. Và Lúc những phần nhỏ này được xếp ông xã lên nhau, bọn chúng tạo ra trở thành một hình trụ to ra thêm. Vì vậy, tất cả chúng ta rất có thể coi diện tích S của hình trụ rộng lớn cũng chính là diện tích S của một hình trụ nhỏ với nửa đường kính R.
Tổng kết lại, diện tích S của hình trụ đó là diện tích S của một hình trụ 2 lần bán kính R, được xem vì chưng công thức S = πR^2.
Xem thêm: concentrate đi với giới từ gì
_HOOK_
Tại sao chu vi hình trụ vì chưng 2 lần bán kính nhân với 3,14 | Học toán thầy Vũ Tiến Thành
Tìm hiểu về chu vi hình trụ vô Clip này! Chúng tôi tiếp tục chỉ dẫn chúng ta qua quýt từng bước đo lường một cơ hội rõ rệt và dễ nắm bắt. Với kỹ năng mới mẻ này, các bạn sẽ rất có thể đo lường chu vi của từng hình trụ một cơ hội đúng chuẩn và đơn giản dễ dàng.
Cách tính diện tích hình tròn | Quý Khách biết không
Xem Clip này nhằm lần hiểu về diện tích S hình trụ và những phần mềm của chính nó vô thực tế! Chúng tôi tiếp tục lý giải cụ thể những công thức tính diện tích S và hỗ trợ những ví dụ thực tiễn nhằm chúng ta có thể vận dụng vô cuộc sống đời thường mỗi ngày.











Bình luận