Diện tích xung xung quanh hình trụ là 1 trong mỗi nội dung cần thiết của môn toán hình học tập không khí. Vậy công thức tính diện tích xung quanh của hình trụ là gì? Ứng dụng của hình trụ nhập cuộc sống thực tiễn? Mời chúng ta theo đuổi dõi nội dung bài viết tiếp sau đây của Hoàng Hà Mobile nhằm hiểu biết thêm những vấn đề thú vị nhé!
Hình trụ là gì?
Trong học tập phần hình học tập không khí, hình trụ được dùng phổ cập, phần mềm nhập những bài bác luyện kể từ cơ bạn dạng cho tới nâng lên. Khi con quay hình chữ nhật ABCD xung quanh cạnh CD một vòng tớ tiếp tục nhận được một hình trụ. Theo cơ, lòng của hình trụ là hình trụ đều bằng nhau và nằm trong phía trên nhị mặt mũi phẳng lặng tuy nhiên tuy nhiên. Trục của hình trụ là cạnh DC và đàng sinh của hình trụ đó là đàng cao. Dựa nhập những Điểm sáng này, những các bạn sẽ tính được diện tích xung xung quanh hình trụ, diện tích S toàn phần hoặc thể tích.
Bạn đang xem: diện tích xung quanh của hình trụ
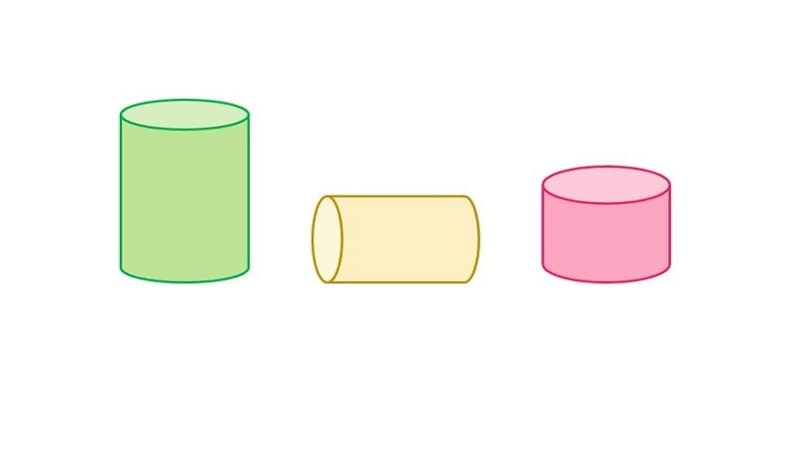
Qua cơ hội phân tích và lý giải bên trên chắc rằng chúng ta đang được tưởng tượng được thế nào là hình trụ. Do hình trụ sở hữu những đặc điểm riêng rẽ như kĩ năng Chịu đựng lực, kĩ năng tàng trữ không khí chất lượng tốt rộng lớn đối với một trong những hình học tập không giống nên những các bạn sẽ phát hiện tương đối nhiều hình học tập này. Một số đồ dùng sở hữu hình trạng trụ như lon nước, đường ống dẫn nước, rường cột.
Các công thức tương quan cho tới hình trụ
Như Shop chúng tôi đang được share phía trên, hình trụ được dùng nhiều nhập cuộc sống thường ngày hằng ngày. Vì vậy, người xem nên biết phương pháp tính diện tích S xung xung quanh, diện tích S toàn phần, thể tích của hình học tập không khí này. Sau phía trên, Shop chúng tôi tiếp tục tổ hợp công thức đo lường tương quan cho tới hình trụ mang đến chúng ta tham ô khảo:
Diện tích xung xung quanh hình trụ
Trước tiên, tất cả chúng ta tiếp tục dò xét hiểu phương pháp tính diện tích xung quanh của hình trụ tức là phần diện tích S mặt mũi xung quanh, ko bao gồm diện tích S của nhị lòng. Để tính diện tích xung quanh của hình trụ, chúng ta hãy lấy chu vi của đàng tròn trặn lòng rồi nhân với độ cao.
Sxq = 2πrh

Trong đó:
- Sxq là diện tích S xung xung quanh.
- 2πr là phương pháp tính chu vi đàng tròn trặn lòng.
- h là độ cao của hình trụ.
Diện tích toàn phần của hình trụ
Tính diện tích S toàn phần của hình trụ tiếp tục bao hàm diện tích S xung xung quanh + diện tích S của nhị mặt mũi lòng. Như vậy, nhằm tính được diện tích S toàn phần của hình trụ, tất cả chúng ta tiếp tục lấy diện tích S xung xung quanh rồi thêm vào đó diện tích S của nhị mặt mũi lòng.
Stp = 2πr^2 + 2πrh

Trong đó:
- Stp – ghi chép tắt của cụm kể từ diện tích S toàn phần.
- 2πr^2 là diện tích S của mặt mũi lòng (đường tròn).
- 2πrh là diện tích xung quanh của hình trụ.
Sau khi dò xét hiểu công thức tính diện tích xung xung quanh hình trụ và diện tích S toàn phần, những chúng ta có thể thấy phương pháp tính khá giản dị. Chúng tôi tiếp tục lấy ví dụ rõ ràng làm cho người xem dễ dàng tưởng tượng rộng lớn nhé!
Bài luyện mang đến hình trụ sở hữu nửa đường kính r = 5cm, độ cao h = 10cm. Yêu cầu tính diện tích S xung xung quanh, diện tích S toàn phần của hình trụ.
Cách giải:
Theo tài liệu của đề bài bác tất cả chúng ta đang được hiểu rằng bánh kính mặt mũi lòng và độ cao hình trụ. Do cơ, tất cả chúng ta chỉ việc vận dụng công thức rồi đo lường đi ra sản phẩm. Diện tích xung xung quanh của hình trụ Sxq = 2πrh = 1 x 3,14 x 5 x 10 = 314 cm2. Sau khi tính được diện tích S xung xung quanh, tất cả chúng ta tiếp tục dò xét diện tích S toàn phần của hình trụ bởi Stp = 2πr^2 + 2πrh = 2 x 3,14 x 5^2 + 314 = 471 cm2.
Thể tích hình trụ
Tính thể tích hình trụ là 1 trong mỗi nội dung nhưng mà chúng ta cần thiết cầm được ở bên cạnh phương pháp tính diện tích xung xung quanh hình trụ, diện tích S toàn phần. Cách tính thể tích của hình trụ cũng tương đối giản dị, chúng ta hãy lấy diện tích S mặt mũi lòng rồi nhân với độ cao.
V = Πr^2h
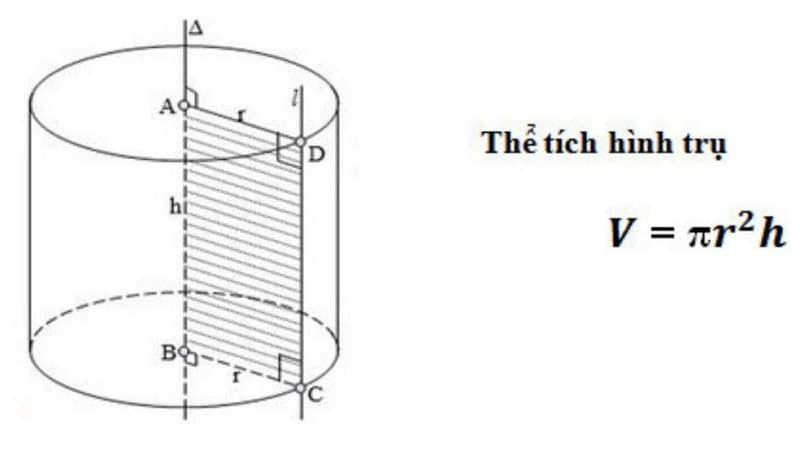
Trong đó:
- V là ký hiệu dùng làm chỉ thể tích của hình trụ.
- πr^2 là diện tích S của mặt mũi lòng.
- h là độ cao của hình trụ.
Để canh ty chúng ta hiểu rộng lớn về kiểu cách tính thể tích hình trụ, Shop chúng tôi tiếp tục lấy ví dụ qua quýt vấn đề rõ ràng. Chẳng hạn như cho 1 hình trụ sở hữu nửa đường kính r = 5cm, độ cao h = 10cm. Thể tích của hình trụ này tiếp tục bởi V = 3,14 x 5^2 x 10 = 785 cm3.
Một số bài bác luyện về hình trụ
Hình trụ là 1 hình học tập không khí được dò xét hiểu nhập học tập phần toán hình lớp 9 và sở hữu tính phần mềm cao. Sau khi dò xét hiểu kỹ năng lý thuyết, sẽ giúp đỡ chúng ta nắm rõ rộng lớn hình trạng học tập này, Shop chúng tôi tiếp tục lấy bài bác luyện minh hoạ, cụ thể:
Bài 1
Cho một hình trụ với chu vi lòng là 8π, độ cao h = 10. Yêu cầu chúng ta hãy tính thể tích của hình trụ.
- 80π
- 40π
- 160π
- 150π
Cách làm:
Để tính được thể tính hình trụ, trước tiên tớ cần thiết tính chu vi lòng. C = 2πr = 8π => r = 4. Như vậy, thể tích hình trụ tiếp tục bởi V = Πr^2h = 160Π => C là đáp án đúng đắn của thắc mắc này.
Bài 2
Một hình trụ xuất hiện lòng nửa đường kính r = 4cm, độ cao h = 5cm. quý khách hãy tính diện tích S xung xung quanh hình trụ đó?
- 40Π
- 30Π
- 20Π
- 50Π
Cách làm: Với bài bác luyện này đang được sở hữu đầy đủ vấn đề, tài liệu của hình trụ, chúng ta chỉ việc vận dụng công thức Sxq = 2πRh = 2π.4.5 = 40π => lựa chọn đáp án A là chuẩn chỉnh xác.
Bài 3
Tiếp tục cho 1 hình trụ sở hữu nửa đường kính lòng r = 8cm và biết tích diện tích S toàn phần bởi 564π cm2. quý khách hãy tính độ cao của hình trụ rồi khoanh nhập đáp án chủ yếu xác?
- 27 cm
- 27,25 cm
- 25 cm
- 25,27 cm
Cách làm: cũng có thể thấy dạng bài bác luyện này đang được sở hữu sự thay cho thay đổi, không giống đối với những bài bác luyện trước cơ. Để tính độ cao của hình trụ, tất cả chúng ta tiếp tục vận dụng công thức:
Stp = 2πr^2 + 2πrh = 256 Π => 16Πh + 2Π8^2 = 564Π => h = 27,25 centimet. Như vậy, tìm kiếm được độ cao của hình trụ bởi 27,25cm -> khoanh nhập đáp án B.
Bài 4
Cho một hình trụ sở hữu nửa đường kính r và độ cao h, nếu như tăng độ cao bên cạnh đó hạn chế nửa đường kính lòng gấp đôi thì:
- Thể tích của hình trụ lưu giữ nguyên
- Diện tích xung xung quanh hình trụ lưu giữ nguyên
- Giữ vẹn toàn diện tích S toàn phần của hình trụ
- Không thay cho thay đổi chu vi lòng hình trụ
Cách làm:
Đầu tiên, tất cả chúng ta tiếp tục xác lập độ cao mới nhất của hình trụ = 2h và nửa đường kính mới nhất là r/2. Dựa nhập phía trên, tất cả chúng ta tiếp tục đi tìm kiếm chu vi lòng = 2Πr’ = 2Π r/2 = Πr < 2Πr = C => D là đáp án sai.
Xem thêm: tổng đài đặt vé xe phương trang
Tiếp tục xét cho tới diện tích S toàn phần của hình trụ:
2ΠR’h + 2ΠR’2 = 2ΠRh + ΠR2/2 không giống với 2ΠRh + 2ΠR2 => B là đáp án sai
Để tính diện tích S toàn phần của hình trụ tớ vận dụng công thức:
2ΠR’h = 2ΠR/2.2h = 2ΠRh => C là đáp án đích thị.
Bài 5
Cho một vỏ hộp sữa ông Thọ đang được vứt nắp sở hữu hình trạng trụ độ cao h = 12cm, 2 lần bán kính lòng là 8cm. Hãy tính diện tích S toàn phần của vỏ hộp sữa ông Thọ.
- 110Π (cm2)
- 128Π (cm2)
- 96Π (cm2)
- 112Π (cm2)
Cách làm:
Với vấn đề đang được mang đến, tất cả chúng ta đơn giản dễ dàng tính được diện tích S toàn phần của vỏ hộp sữa theo đuổi công thức:
Stp = Sxq + Sd = Πdh + Π(d/2)2
= Π.8.12 + Π.(8/2)2 = 112Π (cm2)
=> Chọn D là diện tích S toàn phần của vỏ hộp sữa ông Thọ đang được mang đến.
Bài 6
Cho một hình trụ mang đến nửa đường kính lòng là R và độ cao là h. Nếu tăng độ cao hình trụ lên nhị chuyến bên cạnh đó hạn chế nửa đường kính nhị chuyến thì
- Thể tích hình trụ ko đổi
- Diện tích toàn phần ko đổi
- Diện tích xung xung quanh ko đổi
- Chu vi lòng ko đổi
Cách làm:
Bên cạnh dạng bài bác tính diện tích xung xung quanh hình trụ, chúng ta cần thiết cầm cứng cáp kỹ năng tương quan cho tới hình trạng học tập không khí này. Trước hết, tất cả chúng ta tiếp tục đặt điều độ cao mới nhất mang đến hình trụ là h’ = 2h => kể từ phía trên suy đi ra nửa đường kính mới nhất của mặt mũi lòng được xem là R’ = R/2.
Theo cơ, hình trụ mới nhất sở hữu chu vi lòng 2ΠR’ = 2ΠR/2 = ΠR < 2ΠR = C => đáp án D ko đúng đắn.
Diện tích toàn phần của hình trụ vừa mới được xác định: 2ΠR’h + 2ΠR2 = 2ΠRh + ΠR2/2 không giống với 2ΠR2 => Đáp án B cũng ko đúng đắn.
Tiếp theo đuổi, tất cả chúng ta tiếp tục tính thể tích của hình trụ mới: ΠR’2h = ΠR2h/ 4 không giống với ΠR2h => A cũng chính là đáp án ko đúng đắn.
Cuối nằm trong, tất cả chúng ta tiếp tục tính diện tích xung quanh của hình trụ mới:
2ΠR’h = 2ΠR/2.2h = 2ΠRh => C là đáp án đúng đắn.
Bài 7
Cho hình trụ sở hữu nửa đường kính lòng là R và độ cao là h. Nếu giảm xuống độ cao 9 chuyến bên cạnh đó tăng nửa đường kính lòng lên 3 chuyến thì:
- Thể tích hình trụ ko đổi
- Diện tích toàn phần ko đổi
- Diện tích xung xung quanh ko đổi
- Chu vi lòng ko đổi
Cách làm:
Tương tự động như bên trên, ở dạng bài bác này tớ nên xét hình trụ mới nhất vào cụ thể từng tình huống. Trước hết xác đánh giá trụ mới nhất sở hữu độ cao h’ = h/9 và nửa đường kính lòng mới nhất là R’ = 3R.
Từ phía trên, tất cả chúng ta xác đánh giá trụ mới nhất sở hữu chu vi lòng bằng: 2ΠR’ = 2Π3R = 6ΠR = 3.2ΠR = 3C => D là đáp án ko tính xác.
Tiếp theo đuổi, tính diện tích S toàn phần của hình trụ mới nhất tiếp tục bởi 2ΠR’h + 2ΠR’2 = 2Π3Rh/9 + 2Π (3R) = 2ΠRh/3 + 6ΠRh + 2ΠR2 => B cũng chính là đáp án ko đúng đắn.
Thể tích của hình trụ mới nhất tiếp tục bởi ΠR’2h’ = Π(3R)2h/9 = ΠR2h => A là đáp án đích thị.
Như vậy đáp án thực sự A, tuy vậy để tìm hiểu tại vì sao đáp án C sai thì tất cả chúng ta nối tiếp đo lường. Diện tích xung xung quanh hình trụ mới nhất tiếp tục bởi 2ΠR’h’ – 2Π.3R.h/9 = 2ΠRh/3 không giống với 2ΠRh, bởi vậy C là đáp án sai.
Bài 8
Cho một hình trụ sở hữu nửa đường kính lòng được xác lập bởi 1/4 đàng cao. Nếu hạn chế hình trụ này bởi một phía phẳng lặng trải qua trụ thì mặt phẳng cắt sẽ có được hình chữ nhật với diện tích S là 50cm2. Anh/ chị hãy tính diện tích xung xung quanh hình trụ và thể tích của hình trụ cơ.
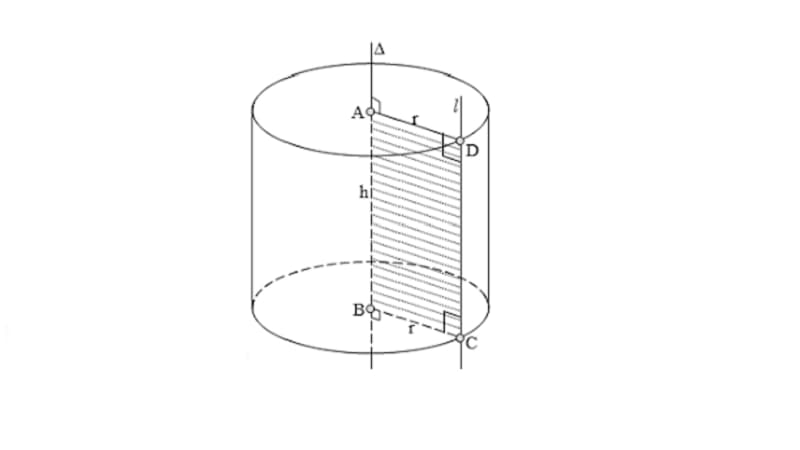
Cách làm:
Theo fake thiết xác lập được nửa đường kính R = 1/4 h nhưng mà diện tích S hình chữ nhật = h.2R = 50cm2. Dựa nhập phía trên tớ sở hữu diện tích S hình chữ nhật = (2.1/4 h).h = 50 => h2 = 100 => h = 10cm. => r = 1/4h = 1/4.10 = 5/2cm.
Do cơ, thể tích của hình trụ tiếp tục bởi ΠR2h = Π(5/2)2. 10 = 62,5Π (cm3)
Xem thêm: chụp ảnh màn hình iphone 11
Diện tích xung xung quanh của hình trụ bởi 2Πrh = 2Π5/2.10 = 50Π (cm2)
Tạm Kết
Như vậy, Shop chúng tôi đang được share phương pháp tính diện tích xung xung quanh hình trụ và những kỹ năng tương quan mang đến chúng ta tìm hiểu thêm. Mong rằng những vấn đề bên trên canh ty chúng ta nhận thêm kỹ năng, khả năng nhằm giải những bài bác luyện về hình trụ. Hãy nối tiếp bấm theo đuổi dõi fanpage facebook Hoàng Hà Mobile và kênh Youtube Hoàng Hà Channel nhằm ko bỏ qua những vấn đề thú vị nhé!
XEM THÊM:
- Công thức tính diện tích S mặt mũi cầu, thể tích khối cầu
- Tìm hiểu công thức tính diện tích S hình tam giác đều, đàng cao tam giác đều











Bình luận