diện tích bề mặt hình cầu

Để tính diện tích S mặt phẳng của một hình cầu, tất cả chúng ta sở hữu công thức:
S = 4πr²
Trong đó:
S là diện tích S mặt phẳng của hình cầu,
π là một trong những hằng số xấp xỉ vị 3.14,
r là nửa đường kính của hình cầu.
Đầu tiên, tớ cần thiết xác lập độ quý hiếm nửa đường kính của hình cầu. Sau cơ, tớ thay cho độ quý hiếm nửa đường kính nhập công thức bên trên nhằm tính được diện tích S mặt phẳng của hình cầu.
Ví dụ: Cho một hình cầu sở hữu nửa đường kính là 10 centimet.
Áp dụng công thức S = 4πr², tớ có:
S = 4 x 3.14 x (10 cm)²
= 4 x 3.14 x 100 cm²
= 1256 cm²
Vậy, diện tích S mặt phẳng của hình cầu với nửa đường kính là 10 centimet là 1256 cm².

Bạn đang xem: diện tích bề mặt hình cầu

Diện tích mặt mũi cầu được xem vị công thức S = 4πR^2, nhập cơ S là diện tích S mặt mũi cầu, π là hằng số Pi có mức giá trị xấp xỉ 3.14 và R là nửa đường kính của hình cầu.
Ví dụ, nhằm tính diện tích S mặt mũi cầu của một hình cầu sở hữu nửa đường kính là 10 centimet, tớ triển khai công việc sau:
1. Sử dụng công thức S = 4πR^2: S = 4 * 3.14 * (10^2) = 4 * 3.14 * 100 = 1256 cm^2.
2. Vậy diện tích S mặt mũi cầu của hình cầu nhập tình huống này là 1256 cm^2.
Tương tự động, nếu như tớ sở hữu vấn đề về 2 lần bán kính của hình cầu, tớ rất có thể tính nửa đường kính R kể từ 2 lần bán kính (R = d/2) rồi vận dụng công thức bên trên nhằm tính diện tích S mặt mũi cầu.
Chúng tớ cũng rất có thể nhận ra rằng diện tích S mặt mũi cầu vị 4 thứ tự diện tích S hình trụ rộng lớn, và vị 4 thứ tự hằng số Pi nhân với bình phương nửa đường kính của hình cầu. Vấn đề này cũng phải chăng với công thức bên trên.

Công thức tính diện tích S mặt phẳng của một hình cầu là S = 4πr^2, nhập cơ S là diện tích S mặt phẳng, π là số pi (gần trúng 3.14) và r là nửa đường kính của hình cầu. Để tính diện tích S mặt phẳng của hình cầu, tớ nhân bình phương của nửa đường kính với 4π. Ví dụ, nếu như nửa đường kính của hình cầu là 10 centimet, diện tích S mặt phẳng của hình cầu này được xem là 4π(10^2) = 400π cm^2.

Đơn vị đo diện tích S mặt phẳng của hình cầu là đơn vị chức năng đo diện tích S thường thì, ví dụ như centimet vuông (cm²) hoặc mét vuông (m²). Để tính diện tích S mặt phẳng của hình cầu, chúng ta cũng có thể dùng công thức sau: S = 4πr², nhập cơ S là diện tích S mặt phẳng, π là số Pi (khoảng 3.14), và r là nửa đường kính của hình cầu.

Để tính diện tích S mặt phẳng của hình cầu khi chỉ biết nửa đường kính, rất có thể dùng công thức sau:
Diện tích mặt phẳng hình cầu = 4πr²
Trong đó:
- Diện tích mặt phẳng hình cầu là sản phẩm cần thiết dò thám.
- π (pi) là một trong những hằng số, có mức giá trị xấp xỉ 3.14159.
- r là nửa đường kính của hình cầu.
Với công thức này, chỉ việc nhân nửa đường kính hình cầu với phiên bản sao của π (pi), tiếp sau đó nhân sản phẩm với 4 nhằm tính được diện tích S mặt phẳng của hình cầu.
Ví dụ: Giả sử nửa đường kính của hình cầu là 10cm.
Áp dụng công thức, tớ có:
Diện tích mặt phẳng hình cầu = 4πr²
= 4 * 3.14159 * 10²
= 4 * 3.14159 * 100
= 1256.636
Vậy diện tích S mặt phẳng của hình cầu khi chỉ biết nửa đường kính là 1256.636 cm².

Có thể tính diện tích bề mặt hình cầu dựa vào 2 lần bán kính. Thứ nhất, tớ cần thiết dò thám nửa đường kính của hình cầu kể từ 2 lần bán kính. Bán kính rất có thể tính vị 1/2 2 lần bán kính của hình cầu.
Sau khi đang được sở hữu nửa đường kính, tớ rất có thể tính diện tích bề mặt hình cầu vị công thức S = 4πr^2, nhập cơ r là nửa đường kính của hình cầu.
Ví dụ, nếu như 2 lần bán kính của hình cầu là 10cm, tớ rất có thể tính nửa đường kính vị 10/2 = 5cm. Tiếp theo đòi, tớ tính diện tích bề mặt hình cầu vị công thức S = 4π(5^2) = 4π25 = 100π cm^2.
Vậy, diện tích bề mặt hình cầu là 100π cm^2.

Để tính diện tích S mặt phẳng của một hình cầu, tớ dùng công thức: S = 4πr^2, nhập cơ S là diện tích S mặt phẳng, π là hằng số Pi (xấp xỉ 3.14), và r là nửa đường kính của hình cầu.
Ví dụ: Giả sử tất cả chúng ta sở hữu một hình cầu sở hữu nửa đường kính là 5 centimet. Để tính diện tích S mặt phẳng của hình cầu này, tớ dùng công thức S = 4π(5^2) = 4π(25) = 100π (cm^2).
Vậy, diện tích S mặt phẳng của hình cầu sở hữu nửa đường kính 5 centimet là 100π (cm^2).

Diện tích mặt phẳng hình cầu tiếp tục thay cho thay đổi theo đòi quy luật chắc chắn khi nửa đường kính của chính nó thay cho thay đổi. Công thức tính diện tích bề mặt hình cầu là S = 4πr^2, nhập cơ r là nửa đường kính của hình cầu. Khi nửa đường kính càng rộng lớn, diện tích S mặt phẳng cầu cũng càng rộng lớn theo đòi tỷ trọng thuận với bình phương nửa đường kính. trái lại, khi nửa đường kính càng nhỏ, diện tích S mặt phẳng cầu cũng càng nhỏ. Vấn đề này Có nghĩa là diện tích S mặt phẳng của hình cầu tăng thêm khi nửa đường kính tăng và giảm xuống khi nửa đường kính rời.

Diện tích mặt phẳng của một hình cầu được xem vị công thức S = 4πR^2, nhập cơ S là diện tích S mặt phẳng của hình cầu, π là số Pi (gần trúng vị 3.14) và R là nửa đường kính của hình cầu.
Để hiểu tại vì sao diện tích bề mặt hình cầu được xem vị 4 thứ tự số Pi nhân với bình phương nửa đường kính, tất cả chúng ta cần thiết lý giải một số trong những định nghĩa tương quan.
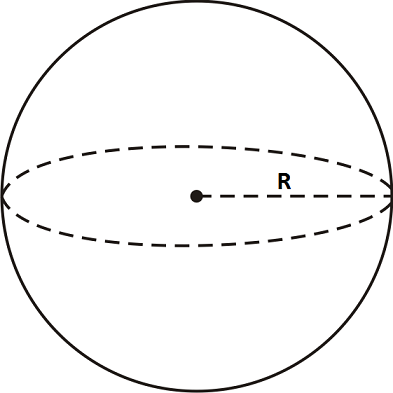
- Hình cầu là một trong những hình vỏ hộp lưu không khí color quan trọng đặc biệt, sở hữu toàn bộ những điểm bên trên mặt mũi cầu cơ hội một điểm xác lập (tâm của hình cầu) một quãng trực tiếp có tính nhiều năm ko vượt lên trước quá nửa đường kính. Đường kính của hình cầu là gấp rất nhiều lần nửa đường kính của chính nó.
- Diện tích mặt phẳng là tổng diện tích S của toàn bộ những mặt mũi mặt của một hình học tập. Trong tình huống hình cầu, diện tích S mặt phẳng là diện tích S của mặt mũi cầu.
Bây giờ, tất cả chúng ta tiếp tục lập luận vì như thế sao diện tích S mặt phẳng của hình cầu được xem vị 4 thứ tự số Pi nhân với bình phương chào bán kính:
1. Đường kính của hình cầu là gấp rất nhiều lần nửa đường kính (d = 2R).
2. Mặt cầu là một trong những hình trụ, và diện tích S hình trụ vị πR^2.
3. Hình cầu sở hữu nhì mặt mũi đối xứng qua loa tâm của chính nó, và từng mặt mũi sở hữu diện tích S là πR^2, vì thế tổng diện tích S của nhì mặt mũi này là 2πR^2.
4. Vì vậy, diện tích S mặt phẳng của hình cầu là nhì thứ tự diện tích S của một phía. Tuy nhiên, khi đo lường diện tích S mặt phẳng của hình cầu, chứ không nhân diện tích S của một phía với 2, tất cả chúng ta dùng số 4 nhằm đo lường diện tích S cho tất cả nhì mặt mũi.
Vì vậy, tất cả chúng ta sở hữu công thức S = 4πR^2 nhằm tính diện tích S mặt phẳng của hình cầu. Công thức này chung tất cả chúng ta đo lường đúng chuẩn và tiện lợi diện tích S mặt phẳng của hình cầu chỉ trải qua nửa đường kính của chính nó.

Xem thêm: đóa hoa của mặt trời

Vâng, rất có thể tính diện tích bề mặt hình cầu khi chỉ biết 2 lần bán kính. Thứ nhất, tất cả chúng ta nên biết mối quan hệ thân thiện 2 lần bán kính và nửa đường kính của hình cầu. Bán kính (R) của hình cầu vị 1/2 2 lần bán kính (d) của chính nó. Vì vậy, tớ sở hữu ông tơ quan lại hệ: R = d/2.
Để tính diện tích S mặt phẳng của hình cầu, tất cả chúng ta dùng công thức: S = 4πR^2.
Bây giờ, hãy kiểm tra một ví dụ ví dụ. Giả sử tất cả chúng ta sở hữu một hình cầu sở hữu 2 lần bán kính d = 10 centimet. Để tính diện tích S mặt phẳng của hình cầu này, tớ cần thiết dò thám nửa đường kính R.
Thay d = 10 centimet nhập quan hệ R = d/2, tớ có: R = 10/2 = 5 centimet.
Tiếp theo đòi, tớ vận dụng công thức S = 4πR^2 nhằm tính diện tích S bề mặt:
S = 4π * (5^2) cm^2 = 4π * 25 cm^2 ≈ 314.16 cm^2.
Vậy, diện tích S mặt phẳng của hình cầu sở hữu 2 lần bán kính 10 centimet là khoảng tầm 314.16 cm^2.