Chu vi hình tam giác đều - Bế Tắc quyết đo lường và tính toán chu vi tam giác chuẩn chỉnh xác
Chủ đề Chu vi hình tam giác đều: Chu vi hình tam giác đều là một trong bộ phận cần thiết nhập toán học tập và hình học tập. Khi toàn bộ những cạnh của tam giác đều phải có phỏng lâu năm cân nhau, công thức của chu vi được dùng là P.. = 3a, với a là phỏng lâu năm của từng cạnh. Việc đo lường và tính toán chu vi tam giác đều gom tất cả chúng ta nắm rõ rộng lớn về những Điểm sáng và tính chất của hình học tập, mặt khác cung ứng một phương pháp để xử lý những việc tương quan cho tới tam giác đều.
Bạn đang xem: công thức tính chu vi tam giác
Chu vi của tam giác đều được xem vì thế công thức nào?
Để tính chu vi của một tam giác đều, tao với công thức sau:
Chu vi tam giác đều = 3 x phỏng lâu năm cạnh tam giác
Với tam giác đều, toàn bộ những cạnh đều phải có phỏng lâu năm cân nhau, chính vì thế, tao chỉ việc tính phỏng lâu năm một cạnh có một không hai và nhân với 3 là sẽ tiến hành chu vi của tam giác đều.
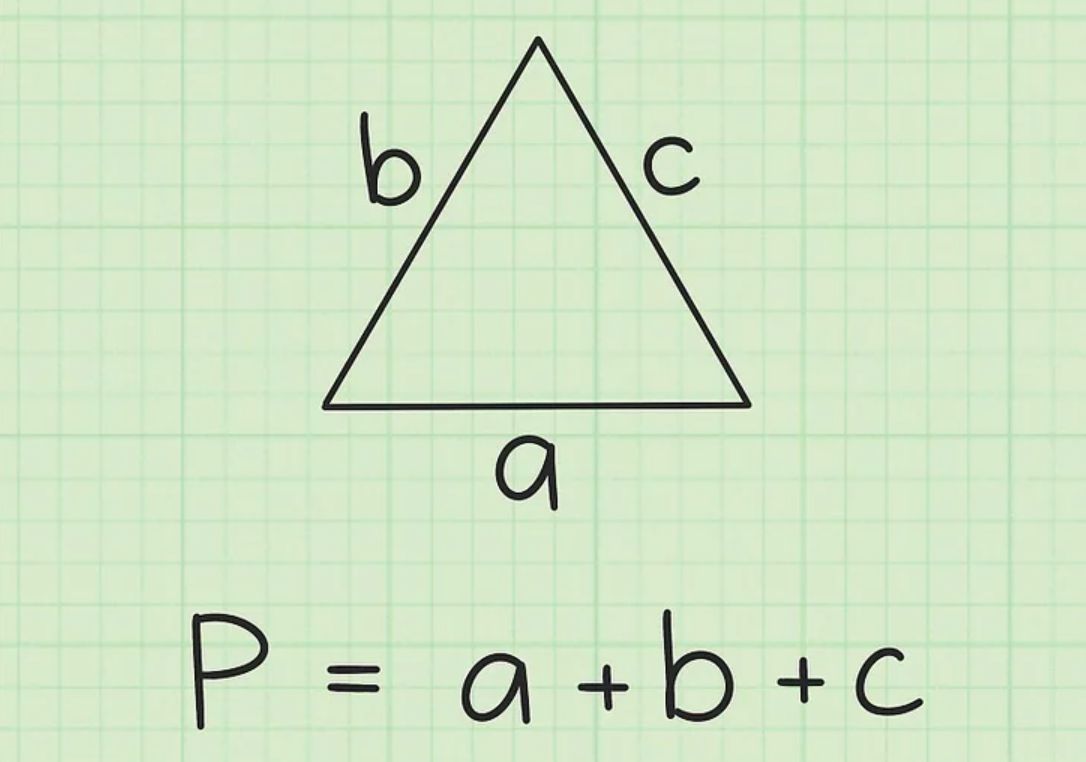
Tam giác này được gọi là tam giác đều?
Tam giác được gọi là tam giác đều Khi toàn bộ những cạnh và toàn bộ những góc cân nhau. Để xác lập một tam giác liệu có phải là tam giác đều hay là không, tao cần thiết đánh giá coi toàn bộ những cạnh có tính lâu năm cân nhau và toàn bộ những góc có tính rộng lớn cân nhau hay là không. Nếu cả tía cạnh và tía góc của tam giác đều phải có phỏng lâu năm và sự cân đối cân nhau, thì tam giác này được gọi là tam giác đều.
Cách tính chu vi của một tam giác đều?
Cách tính chu vi của một tam giác đều là dùng công thức Chu vi tam giác đều = 3 x phỏng lâu năm cạnh.
Bước 1: Xác ấn định phỏng lâu năm của cạnh tam giác. Với tam giác đều, toàn bộ những cạnh có tính lâu năm cân nhau.
Bước 2: Nhân phỏng lâu năm cạnh cho tới số 3. Thực hiện nay phép tắc tính nhân nhằm mò mẫm rời khỏi chu vi tam giác.
Ví dụ: Nếu phỏng lâu năm cạnh tam giác đều là 5cm, tao hoàn toàn có thể tính chu vi như sau: Chu vi tam giác đều = 3 x 5 = 15cm.
Điều này đã cho chúng ta thấy chu vi của tam giác đều là 15cm.

Bạn cũng muốn biết phương pháp tính chu vi của hình tam giác đều không? Hãy coi đoạn Clip này nhằm mò mẫm hiểu phương pháp tính một cơ hội giản dị và nhanh gọn. Quý khách hàng tiếp tục thấy rằng tính chu vi hình tam giác không thể là vấn đề trở ngại nữa!
Công thức tính chu vi tam giác đều là gì?
Công thức tính chu vi của một tam giác đều là chu vi tam giác đều = 3 x a, nhập ê a là phỏng lâu năm một cạnh của tam giác đều.
Để tính chu vi tam giác đều, tao nhân phỏng lâu năm một cạnh của tam giác với số 3. Vì nhập tam giác đều, toàn bộ những cạnh cân nhau nên tao chỉ nên biết phỏng lâu năm của một cạnh nhằm tính được chu vi của tam giác.
Tam giác đều phải có những Điểm sáng gì quánh trưng?
Tam giác đều là một trong loại tam giác đối với cả tía cạnh và cả tía góc cân nhau. Như vậy tức là tam giác đều phải có những bộ phận sau:
1. Cạnh: Các cạnh của tam giác đều phải có nằm trong phỏng lâu năm. Gọi cạnh của tam giác đều là a, thì a được xem là phỏng lâu năm của từng cạnh của tam giác.
2. Góc: Các góc của tam giác túc tắc cân nhau và đều phải có độ quý hiếm 60 phỏng. Như vậy tức là tam giác đều phải có 3 góc vì thế 60 phỏng.
3. Đường cao: Trong tam giác đều, đàng cao của một tam giác đều là đường thẳng liền mạch trải qua trung điểm của một cạnh và vuông góc với cạnh còn sót lại. Tất cả những đàng cao của tam giác đều của tam giác đều trùng nhau và có tính lâu năm vì thế một trong những phần nhì phỏng lâu năm cạnh của tam giác.
4. Chu vi: Chu vi của tam giác đều hoàn toàn có thể tính vì thế công thức Chu vi tam giác đều = 3*a, nhập ê a là phỏng lâu năm của từng cạnh của tam giác.

_HOOK_
Xem thêm: hinh anh loi chuc ngay thu 6
Cách tính chu vi hình tam giác lớp 3 Toán lớp 1-5
Đối với học viên lớp 3, tính chu vi hình tam giác hoàn toàn có thể nhiều lúc khá phức tạp. Nhưng chớ băn khoăn, đoạn Clip này tiếp tục chỉ dẫn các bạn từng bước phương pháp tính chu vi hình tam giác một cơ hội dễ dàng và đơn giản và sống động. Xem ngay lập tức nhằm nắm rõ kỹ năng này!
Làm thế này nhằm tính chu vi của một tam giác đều lúc biết phỏng lâu năm cạnh?
Để tính chu vi của một tam giác đều lúc biết phỏng lâu năm cạnh, tao hoàn toàn có thể dùng công thức P.. = a + b + c, nhập ê a, b, c thứu tự là phỏng lâu năm của những cạnh của tam giác.
Bước 1: Xác ấn định phỏng lâu năm của cạnh tam giác
- Trước tiên, cần thiết xác lập phỏng lâu năm của cạnh của tam giác. Lưu ý rằng nhập một tam giác đều, toàn bộ những cạnh có tính lâu năm cân nhau.
Bước 2: Tính tổng chu vi
- Sau Khi đang được biết phỏng lâu năm của cạnh, tao chỉ việc nằm trong bọn chúng lại cùng nhau nhằm tính tổng chu vi của tam giác. Công thức chu vi tam giác là P.. = a + b + c.
Ví dụ: Giả sử tao biết phỏng lâu năm những cạnh của một tam giác đều là 5 centimet. Ta hoàn toàn có thể tính được chu vi tam giác như sau:
P = a + b + c = 5 + 5 + 5 = 15 centimet.
Vậy nếu như biết phỏng lâu năm cạnh của tam giác đều, tao chỉ việc nằm trong bọn chúng lại nhằm tính chu vi của tam giác.
Vậy nếu như chu vi của tam giác đều là 15cm, phỏng lâu năm từng cạnh là bao nhiêu?
Đầu tiên, nhằm tính chiều lâu năm từng cạnh của tam giác đều lúc biết chu vi là 15cm, tao dùng công thức chu vi tam giác đều: Chu vi tam giác đều = 3 x cạnh tam giác.
Theo công thức bên trên, tao có: 15cm = 3 x cạnh tam giác.
Để mò mẫm độ quý hiếm của cạnh tam giác, tất cả chúng ta phân tách cả nhì vế của phương trình cho tới 3, tao được:
cạnh tam giác = 15cm / 3 = 5cm.
Vậy phỏng lâu năm từng cạnh của tam giác đều là 5cm.
![]()
Tam giác cân nặng giành được xem là tam giác đều không?
Không, tam giác cân nặng ko được xem là tam giác đều.
Tam giác đều là một trong dạng quan trọng của tam giác cân nặng, nhập ê toàn bộ những cạnh đều phải có phỏng lâu năm cân nhau và toàn bộ những góc đều cân nhau. Nhưng tam giác cân nặng chỉ mất nhì cạnh và nhì góc cân nhau, còn một cạnh và một góc ko cân nhau.
Vì vậy, tam giác cân nặng ko thỏa mãn nhu cầu ĐK sẽ được xem là tam giác đều.
Tam giác đều - Hình vuông - Lục giác đều - Môn Toán 6 - Cánh diều - Cô Phương Thu Trang
Tam giác đều, hình vuông vắn, lục giác đều là những định nghĩa nhập môn Toán lớp 6 tuy nhiên những em thông thường gặp gỡ cần. Video này không chỉ có phân tích và lý giải rõ nét kỹ năng này mà còn phải kết phù hợp với ví dụ hài hước về cánh diều và cô Phương Thu Trang. Hãy nằm trong coi và học hành nhé!
Làm sao nhằm tính chu vi của một tam giác cân?
Cách tính chu vi của một tam giác cân nặng là vô cùng giản dị. Trước tiên, tất cả chúng ta phải ghi nhận phỏng lâu năm của nhì cạnh cân nhau, gọi là a. Sau ê, tất cả chúng ta tiếp tục tổ hợp chu vi của tam giác bằng phương pháp nhân phỏng lâu năm cạnh a với 2 và thêm nữa ê phỏng lâu năm cạnh loại tía.
Vì tam giác cân nặng với nhì cạnh cân nhau, nên tam giác cân nặng hoàn toàn có thể được đánh giá như 1 tam giác đều nếu như tao coi nhì cạnh cân nhau là cạnh tam đều của tam giác đều. Do ê, tao hoàn toàn có thể dùng công thức tính chu vi của tam giác đều nhằm tính chu vi của tam giác cân nặng.
Công thức tính chu vi tam giác đều là: chu vi tam giác = a + a + a = 3a, nhập ê a là phỏng lâu năm của cạnh tam giác đều hoặc cạnh tam giác cân nặng.
Vậy, nhằm tính chu vi của một tam giác cân nặng, các bạn chỉ việc nhân phỏng lâu năm của cạnh cân nhau với 3.
Xem thêm: trường đại học kinh tế tài chính tp.hcm
Một tam giác ngẫu nhiên hoàn toàn có thể trở nên tam giác đều không?
Không, một tam giác ngẫu nhiên ko thể trở nên tam giác đều. Một tam giác đều phải có toàn bộ những cạnh với số đo cân nhau và toàn bộ những góc cân nhau. Trong Khi ê, một tam giác ngẫu nhiên hoàn toàn có thể với những cạnh và góc không giống nhau. Để với cùng một tam giác đều, những cạnh của tam giác cần với chiều lâu năm cân nhau và những góc của tam giác cần có mức giá trị cân nhau.
_HOOK_
Cách tính chu vi hình tam giác đều | Toán lớp 1-5
Dành cho tới học viên lớp 1-5, tính chu vi hình tam giác đều hoàn toàn có thể là một trong thử thách. Nhưng chớ lo ngại, đoạn Clip này tiếp tục giúp cho bạn nắm rõ phương pháp tính chu vi hình tam giác một cơ hội dễ dàng và đơn giản qua chuyện những ví dụ thực tiễn và trực quan tiền. Xem ngay lập tức nhằm trở nên Chuyên Viên tính chu vi tam giác!










Bình luận