công thức đường trung tuyến

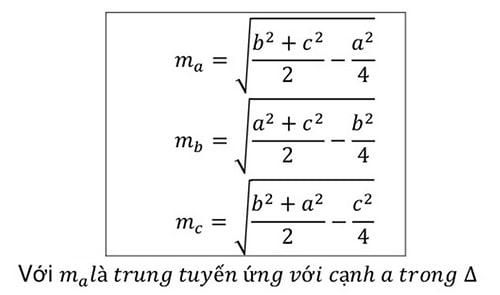
Công thức tính phỏng lâu năm đàng trung tuyến của tam giác là công thức Euclid được xem vì thế công thức nhập hình học:
Đường trung tuyến là đoạn trực tiếp nối trung điểm của nhì cạnh ngẫu nhiên của tam giác với đỉnh sót lại của tam giác. Đường trung tuyến có tính lâu năm vì thế 50% cạnh ứng.
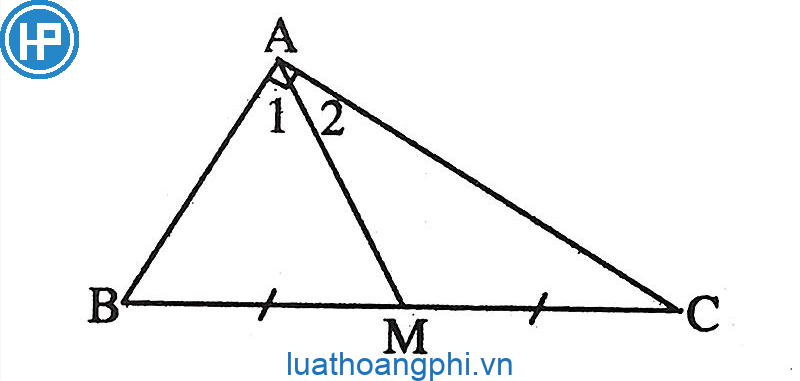
Ví dụ, nhằm tính phỏng lâu năm đàng trung tuyến AM của tam giác ABC, tớ sở hữu công thức:
AM = 50% * BC
Trong công thức bên trên, BC là phỏng lâu năm cạnh BC của tam giác ABC. Ta rất có thể vận dụng công thức tương tự động nhằm tính phỏng lâu năm những đàng trung tuyến không giống của tam giác.

Bạn đang xem: công thức đường trung tuyến

Để tính phỏng lâu năm đàng trung tuyến nhập tam giác, rất có thể dùng công thức sau:
1. trước hết, mò mẫm trung điểm M của cạnh ngẫu nhiên nhập tam giác. Như vậy rất có thể được triển khai bằng phương pháp lấy tổng của nhì tọa phỏng x của nhì đỉnh cuối của cạnh bại liệt và phân tách mang đến 2. Tương tự động, lấy tổng của nhì tọa phỏng nó của nhì đỉnh cuối của cạnh bại liệt và phân tách mang đến 2.
2. Tiếp theo đòi, tính phỏng lâu năm đàng trung tuyến bằng phương pháp tính căn bậc nhì của 1 phần nhì tổng bình phương nhì cạnh kề. Cụ thể, căn bậc nhì của 1 phần nhì tổng bình phương nhì cạnh kề được xem bằng phương pháp lấy căn bậc nhì của tổng bình phương phỏng lâu năm nhì cạnh kề và phân tách mang đến 2.
3. Cuối nằm trong, trừ lên đường 1 phần tư bình phương cạnh đối của đỉnh M (nếu có). Như vậy đáp ứng tính đích phỏng lâu năm đàng trung tuyến.
Với quá trình bên trên, các bạn sẽ giành được phỏng lâu năm đàng trung tuyến nhập tam giác.

Trong công thức tính phỏng lâu năm đàng trung tuyến, quy tắc tính được triển khai thứ nhất là tính tổng bình phương của nhì cạnh kề.

Căn bậc 2 nhập công thức tính phỏng lâu năm đàng trung tuyến ý nghĩa cần thiết trong công việc đo lường. Cụ thể, đấy là phương pháp tính phỏng lâu năm của đàng trung tuyến nhập tam giác.
Theo công thức, phỏng lâu năm đàng trung tuyến được xem vì thế căn bậc 2 của 1 phần 2 tổng bình phương nhì cạnh kề trừ lên đường 1 phần tư bình phương cạnh đối.
Điều này còn có ý tức là căn bậc 2 được dùng nhằm mò mẫm độ quý hiếm đúng mực của phỏng lâu năm đàng trung tuyến. Căn bậc 2 phải chăng được vận dụng vì thế tớ cần thiết mò mẫm phỏng lâu năm thực tiễn của đàng trung tuyến dựa vào độ quý hiếm đàng chéo cánh và cạnh của tam giác.
Việc dùng căn bậc 2 chung tăng tính đúng mực nhập đo lường và đảm nói rằng tất cả chúng ta giành được thành quả đích đắn. Nếu ko dùng căn bậc 2, tất cả chúng ta rất có thể rơi rụng lên đường những độ quý hiếm lẻ nhỏ so với phỏng lâu năm đàng trung tuyến, làm mất đi lên đường sự đúng mực nhập thành quả.
Tóm lại, căn bậc 2 nhập công thức tính phỏng lâu năm đàng trung tuyến ý nghĩa cần thiết trong công việc thể hiện thành quả đúng mực và đích đắn mang đến phỏng lâu năm của đàng trung tuyến nhập tam giác.

Công thức tính phỏng lâu năm đàng trung tuyến là căn bậc nhì của 1 phần nhì tổng bình phương nhì cạnh kề. Tuy nhiên, nhập công thức đó lại sở hữu 1 phần trừ lên đường 1 phần tư bình phương cạnh đối.
Lý bởi cần thiết trừ lên đường 1 phần tư bình phương cạnh đối là nhằm tính đích phỏng lâu năm của đàng trung tuyến. Đường trung tuyến là đoạn trực tiếp nối thẳng từ 1 đỉnh của tam giác cho tới trung điểm của cạnh đối lập. Khi đo lường, tớ ko thể chỉ giản dị và đơn giản lấy căn bình phương cùng theo với căn bình phương của nhì cạnh kề tuy nhiên cần trừ lên đường 1 phần tư bình phương cạnh đối nhằm đáp ứng tính đích đắn của thành quả.
Việc trừ lên đường 1 phần tư bình phương cạnh đối hỗ trợ chúng ta lấy nhập quy tắc tính những nguyên tố quan trọng nhằm đo lường đích phỏng lâu năm của đàng trung tuyến. Như vậy đáp ứng tính đúng mực và uy tín của thành quả Khi dùng công thức tính phỏng lâu năm đàng trung tuyến.

Để tính phỏng lâu năm đàng trung tuyến nhập tam giác cân nặng, tớ rất có thể tuân theo quá trình sau:
Bước 1: Xác ấn định trung điểm của cạnh so với tam giác cân nặng. Khi tam giác cân nặng, tớ hiểu được những cạnh AB và AC sở hữu nằm trong phỏng lâu năm. Vì vậy, tớ rất có thể lấy điểm M là trung điểm của cạnh BC.
Bước 2: Tính phỏng lâu năm đàng trung tuyến. Độ lâu năm đàng trung tuyến được xem vì thế căn bậc 2 của 1 phần 2 tổng bình phương nhì cạnh kề. Cụ thể, tớ tính phỏng lâu năm đàng trung tuyến AM vì thế công thức sau:
Độ lâu năm đàng trung tuyến AM = căn bậc 2 của (1/2 * (AB^2 + AC^2))
Với AB và AC là phỏng lâu năm nhì cạnh kề của tam giác.
Bước 3: Tính toán độ quý hiếm phỏng lâu năm đàng trung tuyến. Thay số nhập công thức và đo lường, tớ sẽ sở hữu độ quý hiếm phỏng lâu năm đàng trung tuyến AM.
Ví dụ: Giả sử AB = AC = 10 centimet (đôi cạnh cân nặng của tam giác) và BC = 12 centimet. Ta tính phỏng lâu năm đàng trung tuyến AM như sau:
Độ lâu năm đàng trung tuyến AM = căn bậc 2 của (1/2 * (10^2 +10^2))
= căn bậc 2 của (1/2 * (100 + 100))
= căn bậc 2 của (200/2)
= căn bậc 2 của 100
= 10 cm
Vậy phỏng lâu năm đàng trung tuyến AM của tam giác cân nặng với nhì cạnh kề có tính lâu năm AB = AC = 10 centimet và cạnh đối BC = 12 centimet là 10 centimet.

Áp dụng công thức tính phỏng lâu năm đàng trung tuyến nhập tam giác vuông, tớ sở hữu quá trình sau:
Bước 1: Xác ấn định tam giác vuông và gọi là những cạnh.
Bước 2: Gọi a, b, c thứu tự là phỏng lâu năm những cạnh của tam giác vuông (với c là cạnh huyền).
Bước 3: Sử dụng công thức phỏng lâu năm đàng trung tuyến: Đường trung tuyến của tam giác vuông vì thế căn bậc 2 của 1 phần 2 tổng bình phương nhì cạnh kề. Sau bại liệt, trừ lên đường 1 phần tư bình phương cạnh đối.
Bước 4: sít dụng công thức: Độ lâu năm đàng trung tuyến nhập tam giác vuông vì thế căn bậc 2 của 1 phần 2 tổng bình phương nhì cạnh góc vuông. Sau bại liệt, trừ lên đường 1 phần tư bình phương cạnh đối.
Bước 5: Tính toán độ quý hiếm mang đến công thức bên trên và triển khai những quy tắc tính quan trọng.
Bước 6: Rút gọn gàng biểu thức và đo lường độ quý hiếm sau cùng.
Với vận dụng công thức tính phỏng lâu năm đàng trung tuyến mang đến tam giác vuông, tớ sẽ sở hữu thành quả rõ ràng dựa vào những độ quý hiếm phỏng lâu năm cạnh của tam giác vuông bại liệt.

Trung điểm là vấn đề tại chính giữa của một quãng trực tiếp. Trong công thức tính phỏng lâu năm đàng trung tuyến của tam giác, trung điểm được dùng là vấn đề tại chính giữa 1 cạnh của tam giác.
Để tính phỏng lâu năm đàng trung tuyến, tớ dùng công thức sau:
Đường trung tuyến = căn bậc 2 của 1 phần 2 tổng bình phương nhì cạnh kề - 1 phần tư bình phương cạnh đối.
Để vận dụng công thức này, tớ cần thiết xác lập trung điểm của một cạnh của tam giác. Đối với tam giác ABC, tớ lựa chọn cạnh AB thực hiện ví dụ. Trung điểm của cạnh AB được ký hiệu là M.
Để mò mẫm trung điểm M, tớ phân tách song cạnh AB và vẽ một đường thẳng liền mạch trải qua M tuy vậy song với cạnh AC. Trung điểm M đó là nút giao của đường thẳng liền mạch này với cạnh AB.
Sau Khi tiếp tục xác lập được trung điểm M, tớ rất có thể dùng công thức bên trên nhằm tính phỏng lâu năm đàng trung tuyến của tam giác ABC.

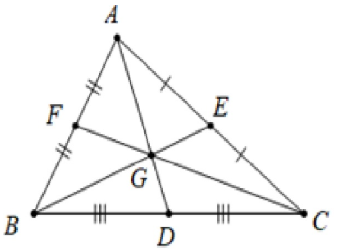
Đường trung tuyến nhập tam giác là đoạn trực tiếp nối một đỉnh của tam giác với trung điểm của cạnh đối lập. Về mặt mũi hình học tập, đàng trung tuyến phân tách cạnh đối lập trở nên nhì phân đoạn đều bằng nhau, và hai tuyến đường trung tuyến chéo cánh nhau bên trên một điểm là trọng tâm của tam giác.
Vai trò của đàng trung tuyến nhập tam giác là nhằm mục tiêu phân loại tam giác trở nên những thành phần đối xứng. Nó hỗ trợ vấn đề về sự việc phẳng phiu của tam giác, địa điểm của trọng tâm, và thêm phần nhập việc giải quyết và xử lý những Việc tương quan cho tới tam giác.
Một số tầm quan trọng của đàng trung tuyến nhập tam giác bao gồm:
1. Đường trung tuyến tách nhau bên trên một điểm gọi là trọng tâm của tam giác, sở hữu tầm quan trọng cần thiết trong công việc xác xác định trí trọng tâm và đặc thù của chính nó.
2. Đường trung tuyến phân tách cạnh đối lập trở nên nhì phần đều bằng nhau, kể từ bại liệt ánh xạ sự phẳng phiu của tam giác.
3. Khi hai tuyến đường trung tuyến tách nhau bên trên một điểm là trọng tâm, tớ rất có thể dùng đỉnh sót lại và điểm tách này nhằm xác lập những địa điểm của những bộ phận không giống của tam giác, như trung điểm, phỏng lâu năm những cạnh, và góc trong những cạnh.
4. Đường trung tuyến cũng rất có thể được dùng nhằm minh chứng những đẳng thức nhập tam giác, như đẳng thức nửa chu vi, nửa đường kính đàng tròn xoe nước ngoài tiếp và nửa đường kính đàng tròn xoe nội tiếp.
Từ những công thức tính phỏng lâu năm đàng trung tuyến, tất cả chúng ta rất có thể đo lường và vận dụng nhập những Việc tương quan cho tới tam giác, từ các việc đo lường những thông số kỹ thuật cơ phiên bản cho tới tìm hiểu những đặc thù hình học tập của tam giác.

Xem thêm: Bắn cá đổi thưởng là gì? Kinh nghiệm chơi bắn cá đổi thưởng luôn thắng

Có những công thức tính phỏng lâu năm đàng trung tuyến không giống nhau giành riêng cho những loại tam giác sau đây:
1. Tam giác nhọn:
- Đường trung tuyến từ 1 đỉnh A tính vì thế nửa căn bậc nhì của tổng bình phương nhì cạnh kề AC và AB trừ lên đường 1 phần tư bình phương cạnh đối A.
- Công thức: AT = sqrt(2 * (AC^2 + AB^2) - BC^2) / 2
2. Tam giác tù:
- Đường trung tuyến từ 1 đỉnh A tính vì thế nửa căn bậc nhì của tổng bình phương nhì cạnh kề AC và AB cùng theo với 1 phần tư bình phương cạnh đối A.
- Công thức: AT = sqrt(2 * (AC^2 + AB^2) + BC^2) / 2
3. Tam giác vuông:
- Đường trung tuyến kể từ đỉnh vuông A tính vì thế nửa căn bậc nhì của tổng bình phương nhì cạnh góc vuông AB và AC.
- Công thức: AT = sqrt(AB^2 + AC^2) / 2
Với AH là đàng trung tuyến kể từ đỉnh A, công thức tính bên trên cũng vận dụng tương tự động cho những đỉnh sót lại của tam giác.