cách tính diện tích tam giác đều

Công thức tính diện tích S tam giác đều là: S = (cạnh^2 * √3) / 4.
Để tính diện tích S tam giác đều, tớ cần phải biết phỏng nhiều năm cạnh tam giác.
Bước 1: Xác lăm le phỏng nhiều năm cạnh tam giác
Trước tiên, tớ cần phải biết phỏng nhiều năm cạnh tam giác đều. Nếu tớ tiếp tục biết phỏng nhiều năm cạnh, tớ hoàn toàn có thể fake cho tới bước tiếp theo sau.
Bước 2: sát dụng công thức tính diện tích S tam giác đều
Công thức tính diện tích S tam giác đều là: S = (cạnh^2 * √3) / 4.
Để tính diện tích S tam giác đều, tớ lấy phỏng nhiều năm cạnh, bình phương nó, nhân với căn bậc nhị của 3, rồi phân tách cho tới 4.
Ví dụ:
Giả sử tớ sở hữu một tam giác đều với phỏng nhiều năm cạnh là 5 centimet.
Ta vận dụng công thức: S = (5^2 * √3) / 4.
S = (25 * √3) / 4.
S = (25 * 1.732) / 4.
S = 43.30 / 4.
S ≈ 10.83 cm^2.
Vậy diện tích S của tam giác đều phải sở hữu phỏng nhiều năm cạnh là 5 centimet là khoảng tầm 10.83 cm^2.

Bạn đang xem: cách tính diện tích tam giác đều

Tam giác đều là một trong những loại tam giác sở hữu Điểm sáng quan trọng đặc biệt, nhập cơ thân phụ cạnh của chính nó có tính nhiều năm đều bằng nhau và toàn bộ những góc nhập tam giác đều phải sở hữu độ quý hiếm vì thế 60 phỏng. Vấn đề này tức là cạnh a, b và c của tam giác đều phải sở hữu độ quý hiếm như nhau. Đặc đặc điểm đó tạo ra một tỉ lệ thành phần quan trọng đặc biệt thân thích chiều nhiều năm cạnh và góc nhập tam giác.
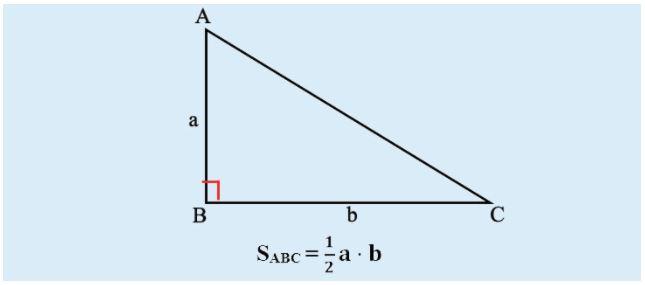
Công thức tính diện tích S tam giác đều được xem trải qua phỏng nhiều năm cạnh và độ cao của tam giác. Với tam giác đều phải sở hữu cạnh a, công thức tính diện tích S là:
Diện tích = (cạnh a)^2 * sqrt(3) / 4
Trong cơ, sqrt(3) là căn bậc nhị của 3.
Bước 1: Tính độ cao của tam giác đều. Chiều cao của tam giác đều là đàng cao kết phù hợp với cạnh lòng tạo nên trở thành một tam giác vuông. Với tam giác đều phải sở hữu cạnh a, độ cao của tam giác là a * sqrt(3) / 2.
Bước 2: Tính diện tích S tam giác đều. Sử dụng công thức tính diện tích S tam giác: Diện tích = (cạnh a) * (chiều cao) / 2. Thay nhập độ quý hiếm cạnh và độ cao ứng, tớ có:
Diện tích = (a) * (a * sqrt(3) / 2) / 2
= (a^2 * sqrt(3)) / 4
Vậy là tớ tiếp tục tính được diện tích S của tam giác đều.

Có một loại công thức tính diện tích S cho tới tam giác đều. Đó là công thức: Diện tích tam giác đều = (cạnh đáy)^2 * √3 / 4. Trong số đó, cạnh lòng là phỏng nhiều năm của những cạnh của tam giác đều.

Công thức tính diện tích S tam giác đều chỉ việc nhờ vào một nguyên tố độc nhất là phỏng nhiều năm cạnh của tam giác. Trong một tam giác đều, toàn bộ những cạnh đều phải sở hữu và một phỏng nhiều năm.
Để tính diện tích S tam giác đều, tớ hoàn toàn có thể dùng công thức sau:
Diện tích = (cạnh)^2 * căn bậc nhị của 3 / 4.
Cùng thực hiện ví dụ nhằm minh họa công thức này. Giả sử tớ sở hữu một tam giác đều phải sở hữu phỏng nhiều năm cạnh là 6 đơn vị chức năng.
Áp dụng công thức, tớ tính được:
Diện tích = (6)^2 * căn bậc nhị của 3 / 4
= 36 * căn bậc nhị của 3 / 4.
Kết ngược sau cùng là diện tích S tam giác đều là 9 căn bậc nhị của 3 đơn vị chức năng vuông.
Như vậy, công thức tính diện tích S tam giác đều chỉ việc nhờ vào phỏng nhiều năm cạnh nhằm đo lường và tính toán. Việc tính diện tích S này là kha khá đơn giản và giản dị và không nhất thiết phải hiểu thêm ngẫu nhiên nguyên tố nào là không giống.

Để tính được phỏng nhiều năm cạnh của tam giác đều, tớ cần phải biết vấn đề rõ ràng tương quan cho tới tam giác như đàng cao, đàng trung tuyến, đàng phân giác, hoặc hình tròn trụ nước ngoài tiếp tam giác. Nhưng nhập tình huống tam giác đều, tất cả chúng ta hoàn toàn có thể vận dụng một số trong những cách thức đơn giản và giản dị.
Phương pháp 1: Kết phù hợp với công thức Pitago
- Xác lăm le đỉnh trung tâm của tam giác đều và vẽ một đường thẳng liền mạch liên kết đỉnh trung tâm với cùng 1 đỉnh ngẫu nhiên của tam giác. Vấn đề này tạo nên trở thành một tam giác vuông, nhập cơ đỉnh trung tâm là đỉnh góc vuông.
- sát dụng công thức Pitago nhằm tính phỏng nhiều năm cạnh của tam giác vuông (hình bên trên được gọi là đàng trung tuyến).
- Với tam giác đều, cạnh của tam giác đó là phỏng nhiều năm của đàng trung tuyến.
Phương pháp 2: Sử dụng những đặc điểm của tam giác đều
- Khi biết phỏng nhiều năm của một cạnh của tam giác đều, tớ hoàn toàn có thể tính được phỏng nhiều năm của những cạnh còn sót lại bằng phương pháp dùng những đặc điểm của tam giác đều.
- Ví dụ, nếu như biết phỏng nhiều năm một cạnh của tam giác đều là a, tớ hiểu được phỏng nhiều năm những cạnh còn sót lại cũng đều vì thế a.
Hy vọng những cách thức đơn giản và giản dị này giúp đỡ bạn tính được phỏng nhiều năm cạnh của tam giác đều một cơ hội đơn giản dễ dàng.

Công thức tính diện tích S tam giác đều là diện tích S lòng nhân với độ cao phân tách cho tới 2 được vận dụng cho tới tam giác đều vì thế những Điểm sáng quan trọng đặc biệt của tam giác này.
1. Tam giác đều phải sở hữu cạnh lòng và độ cao đối xứng cùng nhau. Do cơ, Lúc tớ vẽ một đàng kẻ kể từ đỉnh của tam giác đều cho tới trung điểm của cạnh lòng, tớ sẽ sở hữu được một đàng kẻ vuông góc với cạnh lòng và sở hữu độ cao vì thế với đàng này.
2. Diện tích của tam giác vì thế nửa tích số đàng cao và cạnh lòng. Như tiếp tục trình bày phía trên, độ cao là đoạn trực tiếp kể từ đỉnh của tam giác đều xuống thẳng cho tới trung điểm của cạnh lòng. Do cạnh lòng và độ cao đối xứng cùng nhau, nhân cạnh lòng với độ cao đó là tích của 2 đoạn trực tiếp này.
3. Tuy nhiên, nhập tam giác đều, độ cao lại vì thế đoạn trực tiếp nối thẳng kể từ đỉnh của tam giác cho tới trung điểm cạnh lòng. Như vậy, diện tích S tam giác đều cũng hoàn toàn có thể được xem vì thế diện tích S lòng nhân với đoạn trực tiếp nối thẳng kể từ đỉnh cho tới trung điểm cạnh lòng, rồi phân tách cho tới 2.
Với những đặc điểm và Điểm sáng đối xứng của tam giác đều, công thức tính diện tích S tam giác đều là diện tích S lòng nhân với độ cao phân tách cho tới 2 là một trong những phương pháp tính lênh láng đúng chuẩn và tiện lợi.

Xem thêm: vẽ con vật đơn giản cho be

Có thể người sử dụng công thức không giống nhằm tính diện tích S tam giác đều ko, này đó là dùng công thức Heron. Công thức Heron được dùng nhằm tính diện tích S tam giác ngẫu nhiên dựa vào phỏng nhiều năm những cạnh. Tuy nhiên, với tam giác đều, tớ hoàn toàn có thể người sử dụng công thức cơ bạn dạng độ cao nhân với cạnh lòng phân tách cho tới 2 như tiếp tục nhắc trong số thành phẩm dò xét tìm tòi bên trên Google.
Công thức nhằm tính diện tích S tam giác đều dùng công thức \"diện tích = phỏng nhiều năm độ cao x phỏng nhiều năm cạnh lòng / 2\". Trong tam giác đều, phỏng nhiều năm độ cao là đàng cao từ là 1 đỉnh cho tới cạnh đối lập, và phỏng nhiều năm cạnh lòng là phỏng nhiều năm ngẫu nhiên của cạnh tam giác.
Ví dụ, nếu như tớ sở hữu một tam giác đều với phỏng nhiều năm độ cao là 10 đơn vị chức năng và phỏng nhiều năm cạnh lòng là 8 đơn vị chức năng, tớ hoàn toàn có thể tính diện tích S như sau: diện tích S = 10 x 8 / 2 = 40 đơn vị chức năng vuông.
Tóm lại, nhập tình huống của tam giác đều, công thức tính diện tích S vì thế phỏng nhiều năm độ cao nhân với phỏng nhiều năm cạnh lòng phân tách cho tới 2 là công thức phổ cập và đơn giản và giản dị nhất nhằm tính diện tích S tam giác đều, song, nếu như tiếp tục biết phỏng nhiều năm những cạnh, hoàn toàn có thể vận dụng công thức Heron nhằm tính diện tích S tam giác đều không giống.

Công thức tính diện tích S tam giác đều là (cạnh)^2 x √3 / 4.
Tính diện tích S tam giác thường rất hữu ích và được vận dụng trong tương đối nhiều nghành thực tiễn. Dưới đấy là một số trong những phần mềm thực tiễn của tính diện tích S tam giác đều:
1. Xây dựng và con kiến trúc: Diện tích tam giác đều thông thường được dùng trong những công việc đo lường và tính toán không khí và mặt phẳng cho những công trình xây dựng thi công và phong cách xây dựng. Khi biết diện tích S tam giác đều, người tớ hoàn toàn có thể đơn giản dễ dàng đo lường và tính toán được độ dài rộng và địa điểm của những khối hình không giống nhập một công trình xây dựng.
2. Trang trí và nghệ thuật: Tam giác đều là một trong những hình dạng thích mắt và bằng phẳng, bởi vậy diện tích S tam giác thường rất phù hợp nhằm dùng nhập tô điểm và thẩm mỹ và nghệ thuật. Ví dụ, nhập hoạt động và sinh hoạt tô điểm thiết kế bên trong, người tớ hoàn toàn có thể dùng diện tích S tam giác đều nhằm design dựng những hình dạng tam giác đều nhập không khí.
3. Trong những technology và khoa học: Tính diện tích S tam giác đều cũng khá được dùng rộng thoải mái trong số nghành technology và khoa học tập, như trong những công việc đo lường và tính toán diện tích S của những vùng nhập hình học tập không khí hoặc nhập nghiên cứu và phân tích những hiện tượng kỳ lạ đương nhiên.
4. Thực hiện tại đo lường và tính toán nhập toán học tập và vật lý: Diện tích tam giác đều cũng thông thường được dùng trong số việc nhập toán học tập và vật lý cơ. Ví dụ, diện tích S tam giác đều hoàn toàn có thể được dùng nhằm đo lường và tính toán lực nén nhập cấu tạo hoặc diện tích S của một mặt phẳng cắt qua loa một hình học tập không khí.
5. Kỹ thuật và công nghiệp: Trong nghành nghệ thuật và công nghiệp, tính diện tích S tam giác đều cũng khá được vận dụng nhằm đo lường và tính toán những thông số kỹ thuật nghệ thuật, như diện tích S mặt phẳng của những vật tư hoặc diện tích S của những mặt phẳng hạn chế đối tượng người dùng.
Với những phần mềm thực tiễn này, tính diện tích S tam giác đều góp sức 1 phần cần thiết trong những công việc xử lý những việc và nắm rõ rộng lớn về không khí, hình học tập và những nghành tương quan.

Xem thêm: cách sử dụng google drive

Để đánh giá tính trúng đắn của thành phẩm đo lường và tính toán diện tích S tam giác đều, chúng ta có thể tuân theo quá trình sau:
Bước 1: Xác lăm le phỏng nhiều năm cạnh của tam giác đều. Vì tam giác đều phải sở hữu toàn bộ những cạnh đều bằng nhau, hãy lấy phỏng nhiều năm của một cạnh nhằm dùng nhập quá trình tiếp theo sau.
Bước 2: Sử dụng công thức tính diện tích S tam giác đều. Công thức cho tới diện tích S tam giác đều là: diện tích S = căn bậc nhị của 3 / 4 nhân cạnh bình phương.
Bước 3: Tính toán diện tích S tam giác đều bằng phương pháp vận dụng công thức kể từ bước 2. Hãy chắc hẳn rằng dùng những đơn vị chức năng trúng và đo lường và tính toán đúng chuẩn.
Bước 4: Kiểm tra thành phẩm đo lường và tính toán. So sánh thành phẩm của chúng ta với những thành phẩm đo lường và tính toán kể từ mối cung cấp uy tín hoặc dụng cụ đo lường và tính toán trực tuyến.
Bước 5: Kiểm tra lại quá trình đo lường và tính toán của chúng ta. Xem xét từng bước một nhằm đáp ứng các bạn tiếp tục vận dụng trúng công thức và đo lường và tính toán giá chuẩn trị.
Lưu ý: Khi đo lường và tính toán diện tích S tam giác đều, hãy chắc hẳn rằng dùng công thức đúng chuẩn và trúng đắn. Nếu ko chắc hẳn rằng về kiểu cách tính, hãy dò xét tìm tòi vấn đề kể từ những mối cung cấp đáng tin tưởng hoặc tư vấn kể từ người dân có kiến thức và kỹ năng về toán học tập.